Условие задачи
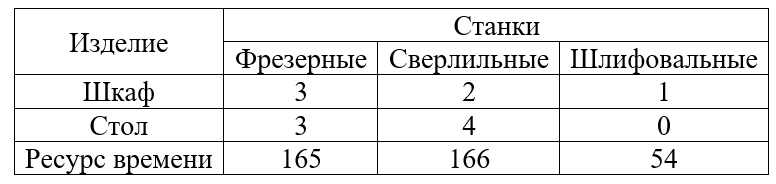
Мебельная фабрика выпускает два вида изделий: шкафы и столы. В производстве применяется оборудование трех типов: фрезерные, сверлильные и шлифовальные станки. Нормы времени работы каждого вида оборудования в час, необходимые для изготовления одного изделия каждого вида, а также ресурсы рабочего времени для каждого вида оборудования известны и приведены в таблице.
Фабрика получает прибыль от изготовления одного шкафа в размере c1 руб. и одного стола – в размере c2 руб. Требуется определить план выпуска изделий каждого вида, при котором время работы оборудования не превышало бы допустимого ресурса, и была получена наибольшая общая прибыль. Исходные данные выбрать из табл.
Составить математическую модель задачи. Решить полученную задачу линейного программирования графически и с помощью надстройки ПОИСК РЕШЕНИЯ в Excel.
Ответ
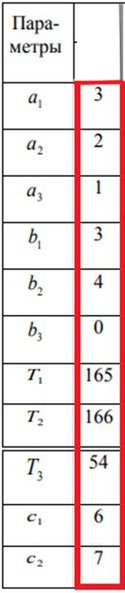
c1 = 6; c2 =7.
Составим экономико-математическую модель задачи.
Пусть x1 количество шкафов, шт.; x2 количество стульев, шт.
Тогда целевая функция есть суммарная прибыль от производства изделий:
F(x) = 6x1 + 7x2 max
При ограничениях на время работы станков:
Фрезерные 3х1 + 3х2 ⩽ 165
Сверлильные 2х1 + 4х2 ⩽ 166
Шлифовальные х1 ⩽ 54
Условие неотрицательности: х1 ⩾ 0; х2 ⩾ 0.
Таким образом,...
