Однородный жёсткий стержень длиной l=1 м и массой M=1 кг свободно висит на горизонтальной идеально гладкой оси вращения О, как показано на рис.
- Физика
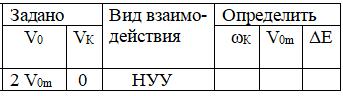
Условие:
Однородный жёсткий стержень длиной l=1 м и массой M=1 кг свободно висит на горизонтальной идеально гладкой оси вращения О, как показано на рис. Ось вращения перпендикулярна плоскости рисунка. Малый шарик массой m=0,1 кг, летящий горизонтально со скоростью V0, движется в плоскости рисунка и ударяет в стержень.
При этом взаимодействие шарика со стержнем может происходить в виде: 
- абсолютно упругого удара (АУУ);
- неупругого удара (НУУ);
- абсолютно неупругого удара (АНУУ).
Сразу после удара стержень вращается с угловой скоростью ω0, а шарик приобретает скорость VК и продолжает двигаться в плоскости рисунка.
Другие исходные данные и искомые величины для каждого варианта задания представлены в таблице.
Расчет следует начинать с определения характерной величины V0m.
V0m – минимальная начальная скорость шарика,
ω0m – соответственно минимальная угловая скорость стержня, при которой стержень после удара совершает полный оборот;
ωК - угловая скорость стержня при прохождении им крайней верхней точки;
φm - максимальный угол отклонения стержня от положения равновесия;
ΔE – потери механической энергии при ударе.
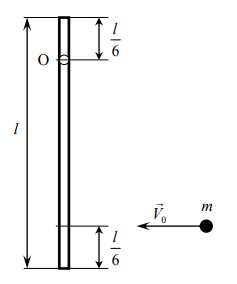
Рис. 3
Решение:
Определим момент инерции стержня относительно оси O, проходящей так, как показано на рисунке 3. Момент инерции стержня относительно оси, перпендикулярной ему и проходящей через центр масс стержня, равняется:
![]()
По теореме Штейнера определим момент инерции стержня относительно осиO на рис. 3. Расстояние от оси, проходящей через центр масс стержня, до осиO равняется
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства