Условие задачи
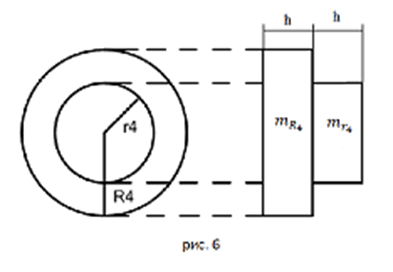
Система, показанная на рисунке 1, состоит из следующих элементов. Грузы массами m1 и m2 движутся поступательно. К грузам прикреплены невесомые нерастяжимые нити, перекинутые или намотанные на блоки массами m3 и m4, которые могут без трения вращаться вокруг горизонтальных осей. Блок массой m3 – сплошной цилиндр, а блок массой m4 – ступенчатый цилиндр с радиусами ступеней r4 и R4 и одинаковой высотой (рисунок 6). При движении по блокам нити не проскальзывают, участки нитей для тел на наклонных плоскостях параллельны этим плоскостям, коэффициент трения тел о любую плоскость равен μ. Система начинает движение из состояния покоя. Считая, что все нити и участки плоскостей имеют достаточную длину, выполнить следующие задания:
Найти ускорения грузов массами m1 и m2 и угловые ускорения блоков ε3, ε4. Принять r3=r4.
Найти силы натяжения всех нитей.
Используя кинематические формулы, найти скорости грузов, угловые скорости блоков и пути, пройденные грузами спустя время τ после начала движения.
Используя закон изменения механической энергии, найти скорости грузов и угловые скорости блоков в тот момент, когда пути, пройденные грузами, составят значения, найдены в п. 3.
Таблица 1
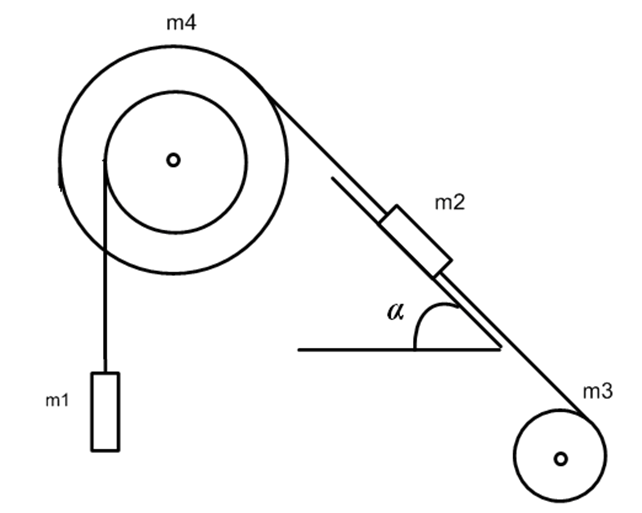
Рисунок 1
Ответ
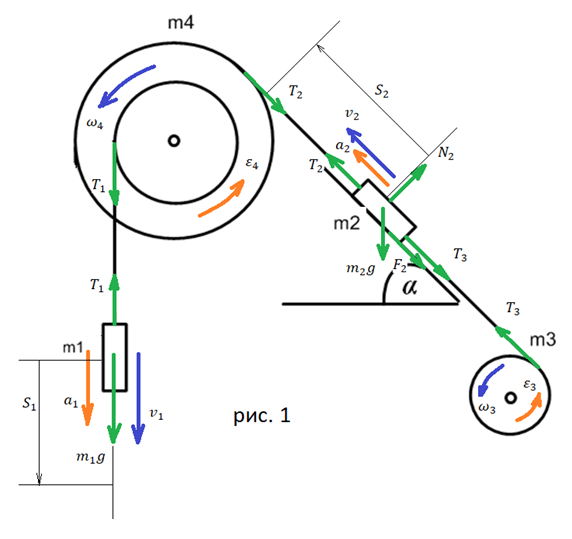
1) Так как m1 намного больше m2, то естественно предположить, что движение произойдет против часовой стрелки. Вращение блоков и движение грузов в соответствующих направлениях будем считать положительными. Вращение блоков обусловлено силами натяжения нитей. Поскольку нити невесомые, то силы натяжения на обоих концах равны (рис. 1). Кроме сил натяжений, на груз 1 действует сила тяжести m1 g, а на гр...
