Прямоугольная пластинка постоянной толщины h с размерами в плане а и b находится под действием внешней поверхностной нагрузки. Требуется: Принять выражение изогнутой поверхности пластинки в виде удерживая в дальнейших расчетах один член ряда m=1, n-1. 1.
- Архитектура и строительство
Условие:
Прямоугольная пластинка постоянной толщины h с размерами в плане а и b находится под действием внешней поверхностной нагрузки.
Требуется:
Принять выражение изогнутой поверхности пластинки в виде
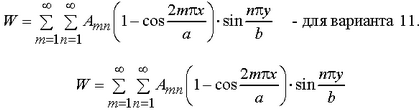
удерживая в дальнейших расчетах один член ряда m=1, n-1.
1. Проверить выполнение граничных условий на контуре пластинки.
2. Определить коэффициент А11 в соответствии с заданным вариационным методом (метод Бубнова-Галеркина).
3. Получить выражения для изгибающих и крутящих моментов и в сечениях 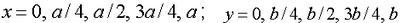 построить их эпюры. Для коэффициента Пуассона принять значение
построить их эпюры. Для коэффициента Пуассона принять значение 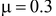 .
.
4. Определить толщину пластинки h из условия прочности в двух вариантах:
а) стальная пластинка - из условия пластичности Мизеса, если 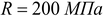 ,
, 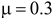 .
.
б) железобетонная пластинка - по теории разрушения Мора, если 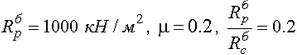
5. Проверить выполнение условия жесткости пластинки, если допускаемое значение прогиба ![]() . Модули упругости принять равными:
. Модули упругости принять равными:
сталь - 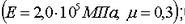 бетон -
бетон - 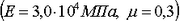
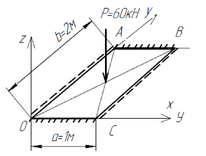
Исходные данные: a=1м b=2м.
Сосредоточенная сила в центре 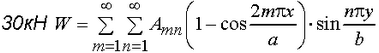
Функция прогибов пластины для n=1 m=1
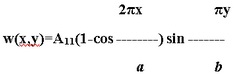
Решение:
Вычисляем дифференциалы уравнения пластины.
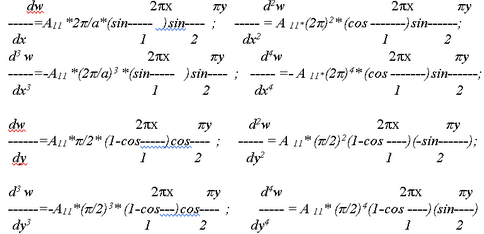
Установим, каким граничным условиям удовлетворяет функция прогибов W(x.y).
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства