Условие задачи
Дано:
Передаточная функция разомкнутой системы Wраз(s)
Исследовать:
По критерию Найквиста устойчивость замкнутой системы. Найти предельное значение коэффициента k=kпред, при котором система находится на границе устойчивости
План решения:
1. По критерию Гурвица (или корневому критерию) определить устойчивость разомкнутой системы.
2. Построить АФЧ разомкнутой системы Wраз(jω)
3. По критерию Найквиста определить устойчивость разомкнутой системы.
4. Найти предельное значение параметра k=kпред, при котором система находится на границе, т.е. АФЧХ разомкнутой системы должна пройти через точку (-1,j0). Для этого из уравнений U(ω)=-1 и V(ω)=0 получить сначала ωпред (из V(ω)=0) и затем, подставив его в U(ω)=-1, найти kпред.
2. По критерию Найквиста исследовать устойчивость замкнутой системы при k=10, если задана передаточная функция соответствующей разомкнутой системы
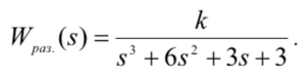
Найти предельное значение коэффициента k=kпред, при котором система находится на границе устойчивости.
Ответ
Исходная передаточная функция разомкнутой системы:
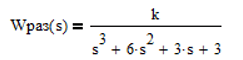
Характеристический полином разомкнутой системы знаменатель ПФ разомкнутой системы:
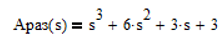
По необходимому условию устойчивости, все коэффициенты характеристи...
