Условие задачи
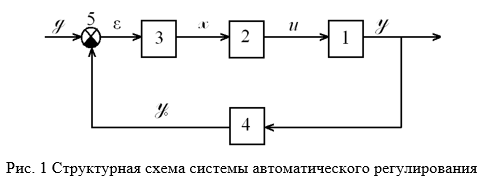
Система автоматического регулирования (рис. 1) состоит из объекта управления 1, исполнительного устройства 2, усилителя 3, датчика 4 и элемента сравнения 5. Подобную структуру может иметь, например, система управления электроприводом, где 1 – электродвигатель, 2 – силовой преобразователь, 3 – усилитель с цепями коррекции, 4 – тахогенератор.
Уравнения элементов системы (p = d/dt):
( 0,04p + 1 )y = 0,1u;
pu = 10x;
( 0,02p + 1 )x = 100ε; y0 = y.
Требуется:
1) определить передаточные функции элементов САР и указать, каким типовым динамическим звеном является каждый из элементов; найти передаточные функции разомкнутой и замкнутой САР;
2) построить амплитудно-фазовую частотную характеристику разомкнутой системы; пользуясь критерием устойчивости Найквиста, определить устойчивость системы в замкнутом состоянии; если система устойчива, то рассчитать запас устойчивости по фазе и по амплитуде;
3) построить логарифмические частотные характеристики разомкнутой системы (асимптотическую амплитудно-частотную и фазо-частотную); определить критическое значение коэффициента усиления разомкнутой системы;
4) составить характеристическое уравнение замкнутой системы; воспользовавшись критерием устойчивости Гурвица определить устойчивость замкнутой САР и критическое значение коэффициента усиления системы в разомкнутом состоянии; результаты сравнить с полученными в п. 2, 3.
Ответ
Часть 1
Зная операторные уравнения, запишем передаточные функции (ПФ) каждого звена:
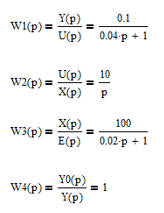
Звенья W1(p) и W3(p) являются апериодическими звеньями 1 порядка; звено W2(p) является идеальным интегрирующим звеном; звено W4(p) является пропорциональным звеном.
Эквивалентная ПФ разомкнутой системы может быть найдена как произведение ПФ всех звеньев, включенных в контур:
