Условие:
Ступень группового искания координатной АТС с индивидуальными управляющими устройствами (маркерами) для каждого блока комплектуется из S коммутационных блоков. Средняя длительность занятия входа ступени ГИ – tвх . На ступень искания поступает нагрузка yвх. Управляющие устройства работают по системе с ожиданием. Средняя длительность занятия одним вызовом управляющего устройства – h , допустимое время ожидания – tдоп.
1. Определить следующие качественные показатели работы управляющих устройств ступени искания при постоянной и экспоненциально распределенной длительности обслуживания:
- вероятность ожидания для поступившего вызова – P{g >0};
- вероятность ожидания свыше допустимого времени t для любого поступившего вызова - P{g >t} при фиксированных значениях .
- вероятность ожидания свыше допустимого времени t для задержанного вызова - P{gз>t} при фиксированных значениях .
- среднее время ожидания для любого поступившего вызова g и задержанного вызова gз
2. Определить среднее число ожидающих вызовов j при экспоненциально распределенной длительности обслуживания.
3. По результатам расчетов построить графические зависимости:
- вероятности P{g >t} от величины t при удельной поступающей нагрузке на управляющее устройство c для постоянной и экспоненциально распределенной длительности обслуживания P{g >t}= f (t) при V=1, c = const;
- вероятности P{gз >t} от величины t при поступающей нагрузке на управляющее устройство c для постоянной и экспоненциально распределенной длительности обслуживания P{gз>t}= f (t) при V=1, c = const;
4. Определить изменения (в процентах) качественных показателей обслуживания {g>t}для фиксированных значений при постоянной и экспоненциально распределенной длительности обслуживания, если нагрузка на ступень искания увеличится на 5%.
Исходные данные :
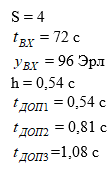
Решение:
1. Нагрузка, поступающая на входы одного блока ГИ, составляет:
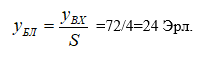
Расчётное значение yp обеспечивает требуемое качество прохождения нагрузки с заданной вероятностью , отклоняясь от математического ожидания нагрузки y по экспоненциальному закону:
