Какая проблема имеет место в 1-м уравнении? Как она проявляется? Для модели (2) проверьте гипотезу о том, что увеличение на 1 минуту расстояния что до метро, что до остановки наземного транспорта, изменяет цену квартиры одинаково.
- Эконометрика
Условие:
Для объяснения продажной цены двухкомнатных квартир (price) в одном из округов некоего мегаполиса из всех таких квартир, проданных в течение одного и того же года, случайным образом были отобраны 52 квартиры. По каждой сделке были получены значения следующих показателей:
price – цена квартиры в млн. рублей,
totsp – общая площадь квартиры в кв.м.,
livsp – жилая площадь квартиры в кв. м.,
walk_t – расстояние до ближайшей остановки наземного транспорта в минутах,
walk_m – время поездки наземным транспортом до станции метро в минутах,
walk – расстояние до станции метро в минутах (walk = walk_m + walk_t).
Были рассчитаны коэффициенты корреляции между всеми парами показателей, причем коэффициент корреляции между totsp и livsp оказался равен 0,92, остальные коэффициенты корреляции по модулю не превосходили 0,5. Отметим также, что между totsp и walk коэффициент корреляции в выборке был равен -0,46.
Далее по МНК были оценены 4 модели, в которых зависимой переменной выступал
логарифм цены квартиры ln (price). (В скобках – стандартные ошибки).
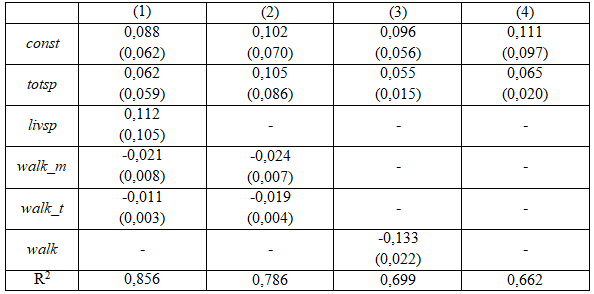
А. Какая проблема имеет место в 1-м уравнении? Как она проявляется?
Б. Для модели (2) проверьте гипотезу о том, что увеличение на 1 минуту расстояния что до метро, что до остановки наземного транспорта, изменяет цену квартиры одинаково.
В. В модели (3) проинтерпретируйте коэффициент при переменной walk. Проверьте гипотезу о том, что коэффициент при totsp больше 0,01.
Г. Можно ли было ожидать заранее, что выбрасывание из модели (3) существенного фактора walk приведет к увеличению оценки при факторе totsp? Ответ обоснуйте соответствующей формулой.
Решение:
n = 52 размер выборки
А.
Теоретическая модель, соответствующая выборочному уравнению (1):
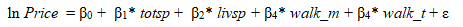
Модель содержит m = 5 параметров
Переменные totsp и livsp в выборке сильно коррелированны (коэфф. корреляции равен 0,92). То есть в 1-м уравнении наблюдается проблема мультиколлинеарности.
Проверим гипотезы о том, что коэффициенты при переменных totsp и livsp значимо отличны от нуля.
1) Коэффициент при переменной ...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства