Условие задачи
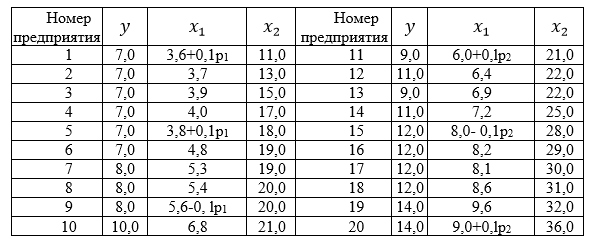
По 20 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от ввода в действие новых основных фондов x1, (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей
численности рабочих x2 (%) (р1 - число букв в полном имени, р2 - число
букв в фамилии).
Требуется:
1. Построить линейную модель множественной регрессии. Записать стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат.
2. Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их
3. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.
4. С помощью F-критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации R2yx1x2.
5. С помощью t-критерия оценить статистическую значимость коэффициентов чистой регрессии.
6. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора x1 после x2 и фактора x2 после x1.
6. Составить уравнение линейной парной регрессии, оставив лишь один значащий фактор.
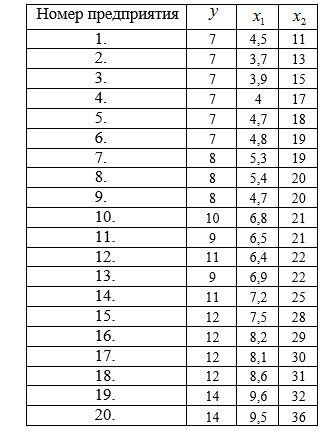
Таблица 1
Исходные данные
Ответ
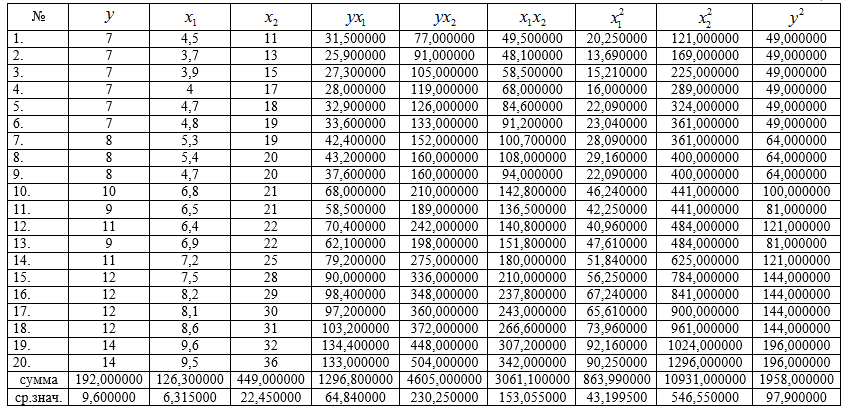
1. Для удобства проведения расчетов поместим результаты промежуточных расчетов в таблицу:
Таблица 2
Найдем средние квадратические отклонения признаков:
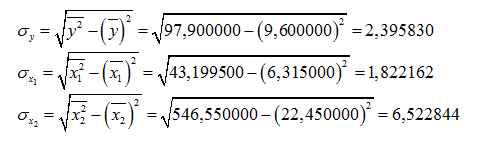
1. Для нахождения параметров линейного уравнения мн...
