На трех базах (пунктах отправления) A1, A2, A3 находится однородный груз в количествах, соответственно равных а1, а2 и а3 единицам. Этот груз требуется перевести в три пункта назначения B1, B2, B3 соответственно в количествах b1, b2 и b3. единиц.
- Экономика
Условие:
Обоснование оптимального плана перевозок груза
На трех базах (пунктах отправления) A1, A2, A3 находится однородный груз в количествах, соответственно равных а1, а2 и а3 единицам. Этот груз требуется перевести в три пункта назначения B1, B2, B3 соответственно в количествах b1, b2 и b3 единиц. Стоимость перевозки единицы груза из i-го пункта отправления в j-й пункт назначения составляет cij денежных единиц.
Определить оптимальный план перевозок, при котором общая стоимость перевозок будет минимальной.
1. Проверить разрешимость транспортной задачи. Если задача не разрешима, свести ее к закрытой задаче введением фиктивного пункта отправления (поставщика) или пункта назначения (потребителя).
2. Построить экономико-математическую модель прямой транспортной задачи и двойственной задачи.
3. Найти начальное решение транспортной задачи и проверить его на вырожденность.
4. Решить транспортную задачу методом потенциалов.
5. Решить транспортную задачу в среде Microsoft Exсel, приложить отчет.
Решение:
1. Проверим разрешимость задачи:
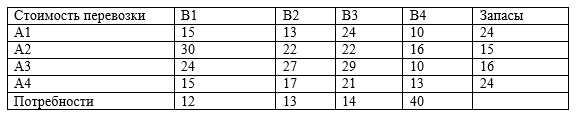
Всего потребности = 12+13+14+40= 79 ед.
Всего запасы = 24+15+16+24= 79 ед.
Задача разрешима, закрытого типа. Запасы полностью потребляются.
2. Строим математическую модель
Пусть:

Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства