Условие задачи
Задача оптимального производства продукции.
Предприятие планирует выпуск двух видов продукции I и II, на производство которых расходуется три вида сырья А, В, С и D. Потребность ij a на каждую единицу j -го вида продукции i -го вида сырья, запас i b соответствующего вида сырья и прибыль j c , от реализации единицы j –го вида продукции заданы таблицей:
1 Для производства двух видов продукции I и II с планом 1 x и 2 x единиц составить целевую функцию прибыли Z и соответствующую систему ограничений по запасам сырья, предполагая, что требуется изготовить в сумме не менее n единиц обоих видов продукции.
2 Найти оптимальный план (х1, х2) производства продукции, обеспечивающий максимальную прибыль Zmax . Определить остатки каждого вида сырья.
Выполнять можно Графическим или Симплекс-методом.
Ответ
1. Пусть х1 количество продукции I вида,
х2 количество продукции II вида.
Тогда - количество ресурса вида А,
- количество ресурса вида B,
- количество ресурса вида C,
- количество ресурса вида D.
По условию задачи ресурсы ограничены, что позволяет составить следующую систему неравенств:
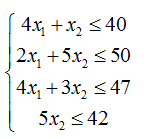
По смыслу задачи:
