Условие задачи
Прядильно-ниточное предприятие выпускает нитки с лавсаном (н/л) и нитки с капроном (н/к), для изготовления которых использует хлопок I сорта (хл.1), а также и хлопок II сорта (хл.2). На изготовление 1 тонны (н/л) требуется 51 кг (хл.1) и 6 кг (хл.2), на изготовление 1 т (н/к) требуется 10 кг (хл.1) и 115 кг (хл.2). Запасы хлопка на предприятии составляют соответственно: 285 кг - (хл.1) и 375 кг - (хл.2).
Прибыль от реализации 1 т (н/л) составляет 729 у.е., а от реализации 1 т (н/к) - 1395 у.е.
Какой должен быть план производства, чтобы суммарная прибыль оказалась максимальной?
Составьте математическую модель этой задачи.
Составьте двойственную к ней задачу, приняв за неизвестные условные цены на хлопок.
Решив обе задачи графическим методом, проверьте выполнение основного принципа двойственности.
Ответ
Пусть х1 объем производства нитки с лавсаном (н/л), т, а х2 объем производства нитки с капроном (н/к), т.
В условии задачи сформулирована цель добиться максимальной прибыли от реализации продукции, поэтому целевую функцию можно сформулировать следующим образом:
.
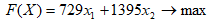Ограничения на использование ресурсов можно записать в виде:
51x1+10x2 285 - по использованию хлопка I сорта, кг.
6x1+115x2 375 - по ...
