Симплексный метод решения задач линейного программирования. Для изготовления различных видов продукции 1, 2, 3 и 4 предприятие использует три вида сырья А, В и С. Нормы расхода сырья на производство единицы

Симплексный метод решения задач линейного программирования

Для изготовления различных видов продукции 1, 2, 3 и 4 предприятие использует три вида сырья А, В и С. Нормы расхода сырья на производство единицы продукции каждого вида, цена одного изделия, а также запас каждого вида ресурса известны и приведены в таблице 1.1.

Составить такой план производства продукции, при котором предприятие получит максимальную прибыль.

Исходные данные задачи выбрать в таблицах 1.1, 1.2 в соответствии с вариантом.

 

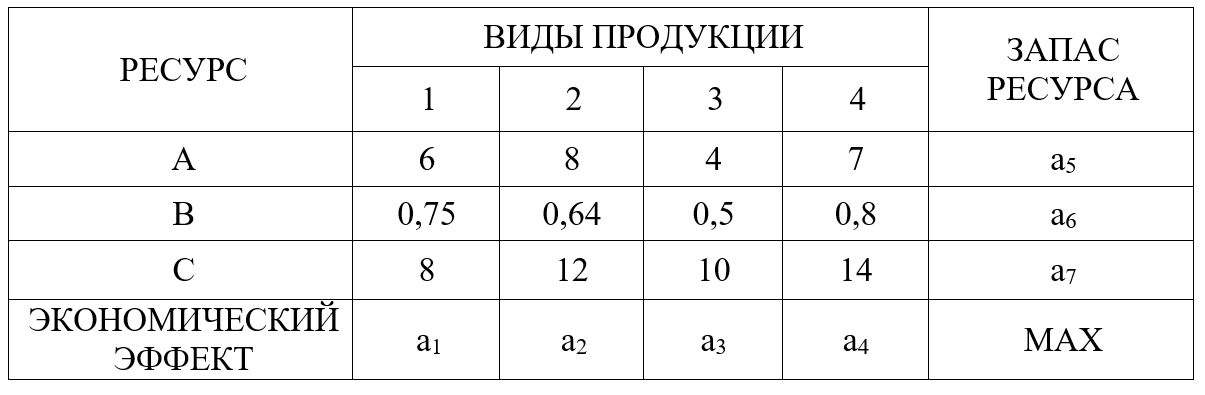
Таблица 1.1 – Нормативы затрат ресурсов на единицу продукции каждого вида

(общие для всех вариантов)

План решения задачи:

·       выбрать из таблиц исходные данные своего варианта;

·       обозначить неизвестные задачи;

·       сформировать систему ограничений и целевую функцию задачи;

·       привести систему ограничений к каноническому виду, обозначив и введя дополнительные переменные;

·       вычертить симплексную таблицу и заполнить её первоначальным опорным планом;

·       пользуясь алгоритмом симплексного метода, найти оптимальное решение задачи;

·       выписать оптимальное решение и провести его экономический анализ.