1. Главная
  2. Библиотека
  3. Физика
  4. Горизонтальная платформа массой М вращается вокруг вертикальной оси, проходящей через центр платформы с частотой n1. Челов...

Горизонтальная платформа массой М вращается вокруг вертикальной оси, проходящей через центр платформы с частотой n1. Человек массой т стоит при этом на краю платформы. Найти частоту вращения платформы n2, если человек пройдет к ее центру.

«Горизонтальная платформа массой М вращается вокруг вертикальной оси, проходящей через центр платформы с частотой n1. Человек массой т стоит при этом на краю платформы. Найти частоту вращения платформы n2, если человек пройдет к ее центру.»
  • Физика

Условие:

Горизонтальная платформа массой М вращается вокруг вертикальной оси, проходящей через центр платформы с частотой n1. Человек массой т стоит при этом на краю платформы.

Найти частоту вращения платформы n2, если человек пройдет к ее центру. Считать платформу однородным диском, а человека - точечной массой.

Решение:

Дано:

М, n1, m

Найти n2

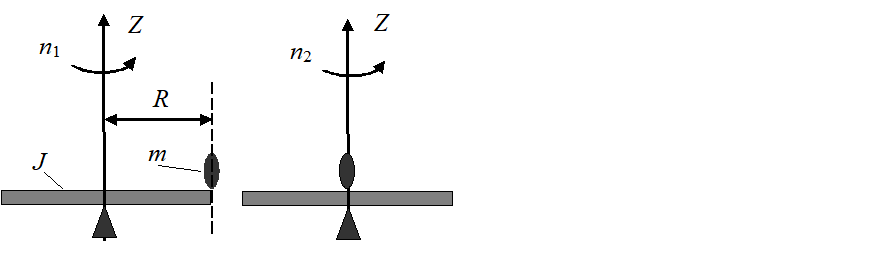
На рисунке представлена динамическая схема задачи.

Систему человек + платформа можно считать изолированной в отношении моментов внешних сил относительно оси вращения (ось z). Поэтому в силу закона сохранения момента импульса, при изменении момента инерции системы, будет меняться и угловая скорость вращения.

Запишем закон сохранения момента импульса относительно оси z:

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я