1. Главная
  2. Библиотека
  3. Физика
  4. Используя метод Фурье вычислить A_k и B_k − амплитуды собственных колебаний закрепленной струны (k=1-5). (∂^2 u)/(∂x^2 )=1...

Используя метод Фурье вычислить A_k и B_k − амплитуды собственных колебаний закрепленной струны (k=1-5). (∂^2 u)/(∂x^2 )=1/v^2 (∂^2 u)/(∂t^2 ), 0<x<2, t≥0, (1) ├ u┤|_(x=0)=0, ├ u┤|_(x=2)=0, (2) ├ u┤|_(t=0)=1-(x-1)^2, ├ ∂u/∂t┤|_(t=0)=0. (3)

«Используя метод Фурье вычислить A_k и B_k − амплитуды собственных колебаний закрепленной струны (k=1-5). (∂^2 u)/(∂x^2 )=1/v^2 (∂^2 u)/(∂t^2 ), 0<x<2, t≥0, (1) ├ u┤|_(x=0)=0, ├ u┤|_(x=2)=0, (2) ├ u┤|_(t=0)=1-(x-1)^2, ├ ∂u/∂t┤|_(t=0)=0. (3)»
  • Физика

Условие:

Используя метод Фурье вычислить Ak и Bk  − амплитуды собственных колебаний закрепленной струны (k=1-5).

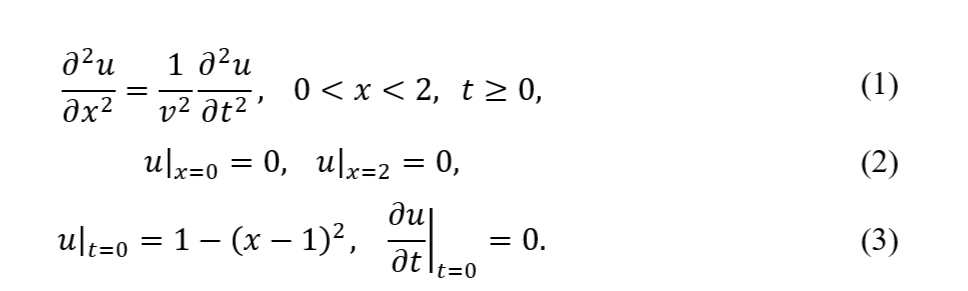
Решение:

Для решения начально-краевой задачи (1) (3) применим метод Фурье разделения переменных. Будем искать нетривиальное решение задачи в виде произведения

u(x,t)=X(x)∙T(t).

Подставим предполагаемую форму решения в исходное уравнение (1)

X'' (x)∙T(t)=1/v2 X(x)∙T'' (t)

Разделим равенство на X(x)∙T(t)

X''(x)/X(x) =(T''(t))/(v2 T(t))=-=const,

т.к. левая часть равенства зависит только от t, а правая только от x.

В результате переменные разделяются, и получается два линейных обыкновенных дифференциальных уравнения

X''(x)+X(x)=0,

T''(t)+v2 T(t)=0,

Подставляя u(x,t) в виде X(x)∙T(t) в граничные условия (2), пол...

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я