Условие:
Внутри сферы радиусом R, на поверхности которой равномерно распределен заряд q1 с поверхностной плотностью σ , находится шар радиусом R/2 , в объеме которого равномерно распределен заряд q2 с объемной плотностью ρ .
Требуется:
1) используя теорему Остроградского-Гаусса, найти зависимость напряженности электрического поля от расстояния;
2) построить график зависимости напряженности электрического поля от расстояния;
3) вычислить напряженность электрического поля в точке, удаленной от центра на расстояние r и указать направление вектора напряженности электрического поля.
Диэлектрическую проницаемость среды считать равной единице.
R = 20 см =0,2 м, σ = 3 нКл/м2= 3 10-9Кл/м2, q2 = 2 нКл=2 10-9Кл, r = 15 м.
Решение:
1) Найдем незаданные величины
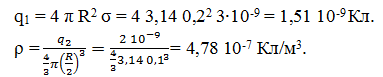
Рассмотрим поле внутри заряженного шара. Сферическая поверхность радиуса r (r R/2) заключает в себе заряд, равный 4/3 r3. Поэтому теорема Остроградского Гаусса для такой поверхности запишется следующим образом
