Условие задачи
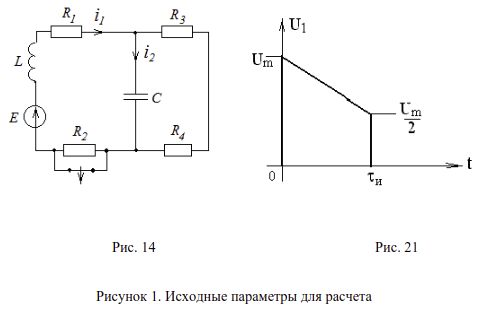
Дана электрическая цепь, в которой происходит коммутация (схемы цепей на рис. 1-20). В цепи действует источник ЭДС. Параметры цепи даны в таблице 1. Требуется:
1. Определить зависимость тока от времени после коммутации в одной из ветвей цепи или напряжения на каком-либо элементе или между заданными точками схемы. Задачу следует решить двумя методами: классическим и операторным, если действует постоянная ЭДС.
2. Заменив постоянную ЭДС в схеме гармонической, частота, амплитуда и начальная фаза которой для каждого варианта даны в таблице 2, решить задачу любым методом.
3. На основании полученных аналитических выражений построить графики искомой величины в функции времени в интервале от t=0 до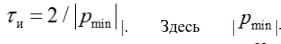 
меньший по модулю корень характеристического уравнения. На графиках показать каждую экспоненту свободной составляющей, их сумму, а также принужденную составляющую после коммутации. Слева от оси ординат изобразить часть до коммутационной составляющей искомой величины (для постоянной и гармонической ЭДС отдельно).
4. Для данной цепи определить комплексную передаточную характеристику (комплексную передаточную проводимость или комплексный коэффициент передачи по напряжению); рассчитать и построить графики амплитудно-частотной и фазочастотной характеристик.
5. Используя операторный метод, определить временные характеристики цепи: переходную h(t) и импульсную g(t) и построить их графики.
6. Используя интегралы Дюамеля, рассчитать и построить отклик цепи на импульсный сигнал, поданный на вход вместо постоянной ЭДС. В таблице 3, в соответствии с номером варианта, указан номер рисунка, на котором приведена форма импульсного сигнала (рис.21-28), а также его амплитуда.
Примечание: 1. Длительность импульса принять равной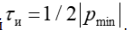 
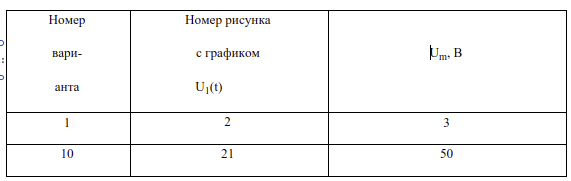
Таблица 1
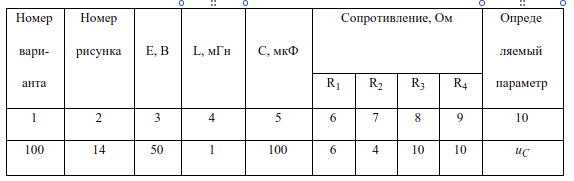
Таблица 2
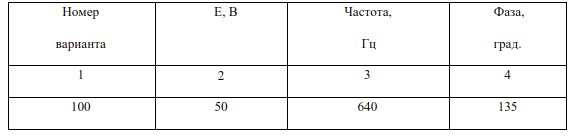
Таблица 3
Ответ
1. Расчет классическим методом при постоянной ЭДС источника напряжения.
а) Определяем независимые начальные условия.
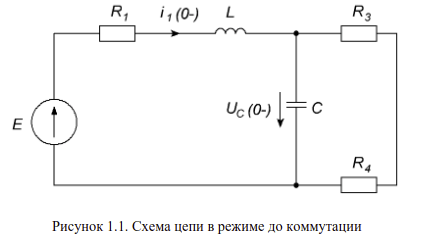
Рассчитываем ток через катушку индуктивности и напряжение на конденсаторе:
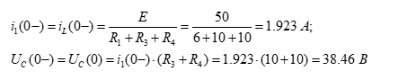
б) Составля...
