Условие:
Сферическая поверхность радиусом R1 = 30 мм имеет равномерно распределенный заряд –5.10-8 Кл. На второй сферической поверхности радиусом R2 = 40 мм равномерно распределен такой же по величине, но положительный заряд. Центры сферических поверхностей совпадают. Все пространство между сферическими поверхностями заполнено однородным диэлектриком ( ε= 5).
Построить графики функций f1(r) и f2(r) для случаев:
I) r < R1 ; 2) R1 ≤ r≤ R2 ; 3) г > R2.
Вычислить разность потенциалов ∆φ между точками r1= 20 мм и r2= 60 мм.
Дано:
R1 = 30 мм = 0,03 м
q1 = –5∙10–8 Кл
q2 = +5∙10–8 Кл
R2 = 40 мм = 0,04 м
ε = 5
r1 = 20 мм = 0,02 м
r2 = 60 мм = 0,06 м
Найти:
Е = f1(r) ― ?
D = f2(r) ― ?
Δφ — ?
Решение:
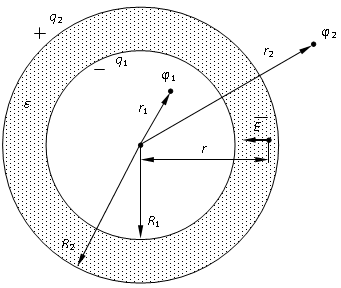
Покажем рисунок.
1) r R1.
Применим теорему Гаусса. Выберем в качестве замкнутой поверхности концентрическую сферу радиуса r R1. Очевидно, что напряженность на поверхности этой сферы будет одинакова по величине и направлена по радиусу. Тогда поток напряженности через нее будет E4r2.
Согласно теореме Гаусса
