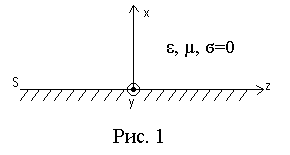
В полупространстве х > 0, ограниченном снизу идеально проводящей плоскостью S (рис. 1), распространяется гармоническая электромагнитная волна. Известны некоторые проекции векторов либо сами векторы поля у этой волны.
- Физика
Условие:
В полупространстве х > 0, ограниченном снизу идеально проводящей плоскостью S (рис. 1), распространяется гармоническая электромагнитная волна. Известны некоторые проекции векторов либо сами векторы поля у этой волны. Они указаны в таблице 1. Параметры среды в полупространстве х > 0 и ряд других параметров поля волны приведены в таблице 2.
Требуется:
1) определить неизвестные проекции либо сами векторы заданного поля волны и охарактеризовать тип волны;
2) проверить выполнение граничных условий на плоскости (поверхности) S;
3) записать выражения для мгновенных значений всех проекций поля волны;
4) записать выражения для мгновенного, комплексного и среднего за период значения вектора Пойнтинга.
5) определить комплексную амплитуду плотности тока, протекающего по поверхности (плоскости) S;
6) рассчитать фазовый коэффициент волны;
7) рассчитать фазовую скорость волны, скорость распространения энергии волны, длину волны;
8) построить зависимости ненулевых мгновенных значений проекции полей волны от координаты х в сечении 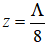 для момента времени
для момента времени 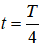 , где Т - период высокой частоты;
, где Т - период высокой частоты;
9) определить потери мощности волны, приходящиеся на единичную площадку поверхности S, если в качестве этой поверхности использовать реальный проводник с удельной проводимостью 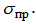
Таблица 1

Таблица 2
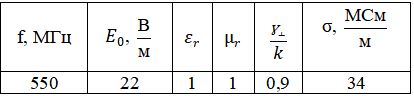
Дано:
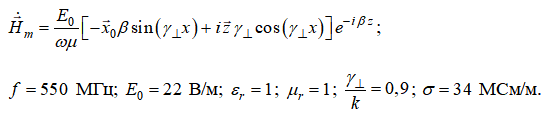
Решение:
1. Проекции вектора 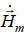 напряженности магнитного поля:
напряженности магнитного поля:
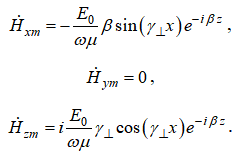
Для определения проекций вектора используем уравнение Максвелла:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства