1. Длина линии при решении обратной геодезической задачи вычисляется по формуле d=√(∆^2+∆y^2) Вычислить расстояние и оценить точность, если ∆x = 3952.34 м, ∆y = 1363.67 м, m_∆x = 0.29 м, m_∆y = 0.17 м. 2. Вычислить относительную среднюю
- Геодезия
Условие:
1. Длина линии при решении обратной геодезической задачи вычисляется по формуле

Вычислить расстояние и оценить точность, если ∆x = 3952.34 м, ∆y = 1363.67 м, m∆x = 0.29 м, m∆y = 0.17 м.
2. Вычислить относительную среднюю квадратическую ошибку измерения длины линии s = 15 892.48 м, если истинные ошибки равны -13.4 см; -15.8 см; +12.9 см; +14.3 см; +11.8 см; +14.9 см; -13.8 см.
3. Вычислить значение функции Ф = 321.05 · 8.03, оценить её точность и правильно записать результат.
4. Вычислить среднюю квадратическую ошибку суммарного влияния случайных и систематических ошибок при измерении базиса длиной 20 м жезлом 2 м, если случайная средняя квадратическая ошибка измерения одним жезлом m∆ = 0.1 мм, а систематическая mδ = 0.01 мм.
Решение:
1. 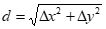
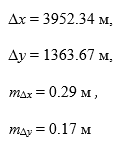
Средняя квадратическая погрешность определяется по формуле:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства