Решение задачи
Докажите, что центр окружности лежит на серединном перпендикуляре к любой ее хорде. лежит на серединном перпендикуляре. Что и требовалось доказать.
- Геометрия
Условие:
Докажите, что центр окружности лежит на серединном перпендикуляре к любой ее хорде. рис 3.
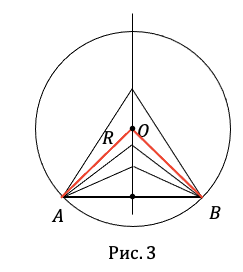
Решение:
По свойству серединного перпендикуляра отрезка точки серединного перпендикуляра произвольной хорды (рис.3) равноудалены от его концов и любая другая точка, не лежащая на серединном перпендикуляре, не обладает этим свойством. Отсюда следует, что т.к. являются точками окружности, и то точка лежит на серединном перпендикуляре.
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
Р
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э