База задач по геометрии
Свыше 2 миллионов материалов для учебы
Пример задачи: «Два маленьких массивных шарика закреплены на концах невесомого стержня длины d. Стержень может вращаться в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня...»
- Материалы со всех ВУЗов страны
- Примеры, чтобы разобраться
- 160+ дисциплин в базе
- 2 000 000+ решенных задач
Список решенных задач
Билет на автобус стоит 30 рублей. Определите, на сколько поездок хватит 100 рублей, если стоимость билета снизят на десять процентов.
Билет на автобус стоит 30 рублей. Определите, на сколько поездок хватит 100 рублей, если стоимость билета снизят на 10%.
Геометрия
Найти объём многогранника, вершинами которого являются точки A,A1, B1, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 6 см2, а боковое ребро равно 4 см.
Найти объём многогранника, вершинами которого являются точки A,A1, B1, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 6 см2, а боковое ребро равно 4 см.
Геометрия
Даны вершины пирамиды А1 А2 А3 А4. Найдите: 1) длину ребра А1А2 2) угол между ребрами А1А2 и А1А3 3) площадь грани А1А2А3 4) объем пирамиды 5) уравнение прямой А1А2 6) уравнение плоскости А1А2А3
Даны вершины пирамиды А1 А2 А3 А4. Найдите:
1) длину ребра А1А2
2) угол между ребрами А1А2 и А1А3
3) площадь грани А1А2А3
4) объем пирамиды
5) уравнение прямой А1А2
6) уравнение плоскости А1А2А3
А1(2,-2,4), А2(5,1,-1), А3(6,-1,3), А4(3,2,-2).
Геометрия
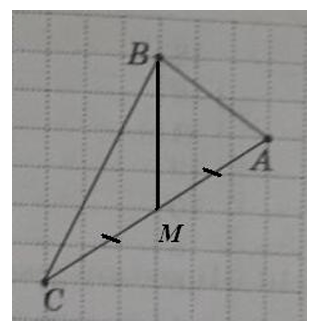
На клетчатой бумаге с размером клетки 1×1 изображен треугольник . Найдите длину его медианы, проведенной к стороне .На клетчатой бумаге с размером клетки 1×1 изображен треугольник . Найдите
На клетчатой бумаге с размером клетки 1×1 изображен треугольник АВС. Найдите длину его медианы, проведенной к стороне АС.
.
Геометрия
Радиус основания цилиндра равен 2,5см, образующая - 5см. Найдите площадь осевого сечения цилиндра: а) 25см2; б) 12,5см2; в) 10см2; г) 25πсм2.
Радиус основания цилиндра равен 2,5см, образующая - 5см. Найдите площадь осевого сечения цилиндра:
а) 25см2; б) 12,5см2; в) 10см2; г) 25πсм2.
Геометрия
Сфера задана уравнением . а) Определите координаты центра сферы и ее радиус. б) Определите, принадлежат ли точки и данной сфере.
Сфера задана уравнением
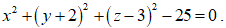
а) Определите координаты центра сферы и ее радиус.
б) Определите, принадлежат ли точки
 данной сфере.
данной сфере.Геометрия
4.1. В каком случае отрезок проецируется в натуральную величину? 4.2. В каком случае отрезок проецируется в точку? 4.3. В каком случае проекция отрезка меньше натуральной величины?
4.1. В каком случае отрезок проецируется в натуральную величину?
4.2. В каком случае отрезок проецируется в точку?
4.3. В каком случае проекция отрезка меньше натуральной величины?
4.3. В каком случае проекция отрезка больше натуральной величины?
4.4. В каком случае проекцией отрезка является отрезок?
4.5. В каком случае проекция отрезка параллельна самому отрезку?
4.6. В каком случае отрезок проецируется не в натуральную величину?
4.7. В каком случае отрезок проецируется не в точку?

4.8. Если координата z всех точек отрезка одинакова, то отрезок параллелен какой оси проекций?
4.9. Если координата х всех точек отрезка одинакова, то отрезок параллелен какой оси проекций?
4.10. Если координата у всех точек отрезка одинакова, то отрезок параллелен какой оси проекций?
4.11. Если координаты z и х всех точек отрезка одинаковы, то отрезок перпендикулярен какой плоскости проекций?
4.12. Если координаты z и у всех точек отрезка одинаковы, то отрезок перпендикулярен какой плоскости проекций?
4.13. Если координаты х и у всех точек отрезка одинаковы, то отрезок перпендикулярен какой плоскости проекций?
4.14. Если координаты х и у всех точек отрезка одинаковы, то отрезок параллелен каким плоскостям проекций?
4.15. Если координаты х и z всех точек отрезка одинаковы, то отрезок параллелен каким плоскостям проекций?
4.16. Если координаты z и у всех точек отрезка одинаковы, то отрезок параллелен каким плоскостям плоскости проекций?

4.17. На каком эпюре изображена прямая, расположенная в профильной плоскости проекций?
4.18. На каком эпюре изображена прямая, параллельная профильной плоскости проекций?
4.19. На каком эпюре изображена прямая, расположенная в фронтальной плоскости проекций?
4.20. На каком эпюре изображена прямая, параллельная фронтальной плоскости проекций?
4.21. На каком эпюре изображена прямая, расположенная в горизонтальной плоскости проекций?
4.22. На каком эпюре изображена прямая, параллельная горизонтальной плоскости проекций?
4.23. На каком эпюре изображена прямая общего положения?
4.24. На каком эпюре изображена прямая, перпендикулярная горизонтальной плоскости проекций?
4.25. На каком эпюре изображена прямая, перпендикулярная фронтальной плоскости проекций?
4.26. На каком эпюре изображена прямая, перпендикулярная профильной плоскости проекций?
4.27. На каком эпюре изображена прямая общего положения, пересекающая ось проекций Ox?
4.28. На каком эпюре изображена прямая общего положения, пересекающая ось проекций Oy?
4.29. На каком эпюре изображена прямая общего положения, пересекающая ось проекций Oz?
4.30. На каком эпюре изображена фронтально проецирующая прямая?
4.31. На каком эпюре изображена горизонтально проецирующая прямая?
4.32. На каком эпюре изображена профильно проецирующая прямая?

Геометрия
1. Радиус основания цилиндра равен 2 см, высота – 5 см, тогда площадь боковой поверхности равна: В цилиндре радиуса осевым сечением является квадрат, а площадь основания равна 16p кв.дм. Найдите площадь боковой поверхности цилиндра.
1. Радиус основания цилиндра равен 2 см, высота – 5 см, тогда площадь боковой поверхности равна:
4π
10 π
20π
40π2. В цилиндре радиуса осевым сечением является квадрат, а площадь основания равна 16p кв.дм. Найдите площадь боковой поверхности цилиндра.
80π
96 π
64 π
32π3.Радиус основания цилиндра в два раза меньше образующей, равной 4, тогда площадь боковой поверхности равна:
4π
32π
16π
8π4. Площадь полной поверхности цилиндра, полученного вращением прямоугольника со сторонами 4 см и 7 см вокруг его большей стороны, равна:
56 π
72π
88π
48 π5. Если площадь боковой поверхности цилиндра равна 64p кв.м, а высота – 4 м, тогда радиус равен:
26
8
16
8π6. Осевым сечением цилиндра является прямоугольник со сторонами 10 и 16 см, то площадь основания цилиндра может быть равна:
64 π
100 π
24 π
256π7. Во сколько раз увеличится площадь боковой поверхности цилиндра, если его высоту и радиус увеличить в три раза?
3
6
9
278. Осевым сечением цилиндра является прямоугольник со сторонами 12 и 8 см, то площадь боковой поверхности цилиндра может быть равна:
64π
36 π
48 π
96 π9. Во сколько раз уменьшится площадь боковой поверхности цилиндра, если его высоту уменьшить в 4 раза а радиус увеличить в 2 раза?
не изменится
8
4
210. Во сколько раз увеличится площадь боковой поверхности цилиндра, если его высоту уменьшить в 3раза а радиус увеличить в 12 раз?
8
6
не изменится
4Геометрия
В правильной треугольной пирамиде SABC точка М-середина ребра АВ, S-вершина. Известно, что ВС=3, а площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка SM
В правильной треугольной пирамиде SABC точка М-середина ребра АВ, S-вершина. Известно, что ВС=3, а площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка SM
Геометрия
Даны вершины пирамиды . Найти: а) угол между гранями ABC и ABD; б) каноническое и параметрические уравнения прямой CD; в) уравнение плоскости параллельной плоскости ABС, проходящей через точку D; г) каноническое уравнение высоты пирамиды.
Даны вершины пирамиды
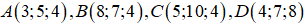 . Найти:
. Найти:а) угол между гранями ABC и ABD;
б) каноническое и параметрические уравнения прямой CD;
в) уравнение плоскости параллельной плоскости ABС, проходящей через точку D;
г) каноническое уравнение высоты пирамиды.
Геометрия
Найти объем треугольной пирамиды с вершинами А(два, два, два), В(четыре, три, три), С(четыре, пять, четыре), D(пять, пять, шесть). Найти объем
Найти объем треугольной пирамиды с вершинами А(2,2,2), В(4,3,3), С(4,5,4), D(5,5,6).
Геометрия
Вычислить площадь фигуры, ограниченной параболой и прямой. Сделать чертеж и заштриховать искомую площадь. Найдем координаты точек пересечения параболы и прямой, решив систему их уравнений, и построим полученные точки в системе
Вычислить площадь фигуры, ограниченной параболой и прямой. Сделать чертеж и заштриховать искомую площадь.
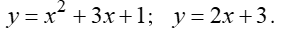
Геометрия
Даны вершины A(–2; –3), B(0; 2), C(3; –3) треугольника ABC. Найти 1) уравнения сторон треугольника и их длины; 2) величину внутреннего угла A в радианах
Даны вершины A(–2; –3), B(0; 2), C(3; –3) треугольника ABC. Найти
1) уравнения сторон треугольника и их длины;
2) величину внутреннего угла A в радианах с точностью до 0,01;
3) уравнение медианы, проведенной из вершины A;
4) точку пересечения медиан треугольника;
5) уравнение высоты, проведенной через вершину A;
6) длину высоты, проведенной через вершину A. Сделать чертеж.
Геометрия
Найти площадь фигуры, ограниченной данными линиями. Площадь фигуры, ограниченной кривыми в полярных координатах вычисляется по формуле
Найти площадь фигуры, ограниченной данными линиями.

Геометрия
Даны вершины треугольника Найти: 1) длину стороны 2) уравнение стороны 3) уравнение высоты и ее длину; 4) уравнение окружности
Даны вершины треугольника
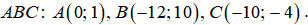
Найти:
1) длину стороны

2) уравнение стороны

3) уравнение высоты
 и ее длину;
и ее длину;4) уравнение окружности, для которой высота
 является диаметром.
является диаметром.Геометрия
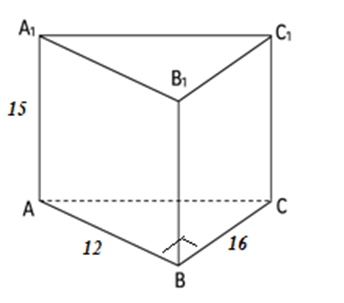
В основании прямой призмы лежит прямоугольный треугольник с катетами AB = 12 см и BC = 16 см (см. рис.). Высота призмы равна 15 см. а) Найдите объём данной призмы.
В основании прямой призмы лежит прямоугольный треугольник с катетами AB = 12 см и BC = 16 см (см. рис.). Высота призмы равна 15 см.
а) Найдите объём данной призмы.
б) Постройте сечение, проходящее через ребро BB1 и середину стороны AC. Укажите название фигуры, которая является сечением.
в) Найдите площадь этого сечения.
Геометрия
Составить уравнения сторон треугольника, зная одну его вершину C(четыре; минус один), а также уравнения высоты 2x-3y+12=0, медианы 2x+3y=0.
Составить уравнения сторон треугольника, зная одну его вершину C(4;-1), а также уравнения высоты 2x-3y+12=0, медианы 2x+3y=0.
Геометрия
Даны две смежные вершины параллелограмма В(3,-4), С(2,-3) и точка пересечения диагоналей М(-2,0). Найти другие вершины.Диагонали делятся точкой пересечения пополам. То есть точка А имеет координаты
Даны две смежные вершины параллелограмма В(3,-4), С(2,-3) и точка пересечения диагоналей М(-2,0). Найти другие вершины.
Геометрия
Высота цилиндра равна восемь см, а площадь его боковой поверхности втрое меньше площади его полной поверхности. Найти объем цилиндра.
Высота цилиндра равна 8 см, а площадь его боковой поверхности втрое меньше площади его полной поверхности. Найти объем цилиндра.
Геометрия
Дано: Сила F расположена в одной из граней прямоугольного параллелепипеда. Модуль силы F, углы α и β следует считать известными. Чему равна проекция силы F на ось u ?
Дано: Сила F расположена в одной из граней прямоугольного параллелепипеда.
Модуль силы F, углы α и β следует считать известными.
Чему равна проекция силы F на ось u ?

Выберите один ответ:
a. Fu=cosα*sinβ
b. Fu=-cosα*cosβ
c. Fu=-sinα*cosβ
d. Fu=sinα*sinβ
Геометрия
Стороны AB, AC равнобедренного треугольника ABC равны 5 см и лежат в двух перпендикулярных плоскостях. Точки B, C удалены от прямой пересечения плоскостей на 4 см. Найти площадь треугольника.
Стороны AB, AC равнобедренного треугольника ABC равны 5 см и лежат в двух перпендикулярных плоскостях. Точки B, C удалены от прямой пересечения плоскостей на 4 см.
Найти площадь треугольника.
Геометрия
В параллелограмме KLMN каждый из углов LKM и MNL равен 57°. Определите, является ли параллелограмм прямоугольником. Обозначим точку пересечения диагоналей О.
В параллелограмме KLMN каждый из углов LKM и MNL равен 57°. Определите, является ли параллелограмм прямоугольником.
Геометрия
Привести уравнение кривой второго порядка к каноническому виду. Для эллипса найти координаты вершин и фокусов, для гиперболы – координаты вершин, фокусов и уравнения асимптот, для параболы – координаты фокуса и
Привести уравнение кривой второго порядка к каноническому виду. Для эллипса найти координаты вершин и фокусов, для гиперболы – координаты вершин, фокусов и уравнения асимптот, для параболы – координаты фокуса и уравнение директрисы, для окружности – координаты центра и радиус. Сделать чертеж.

Геометрия
Даны координаты вершин пирамиды ABCD. Найти: 1. уравнения ребер АВ, АС и AD; 2. уравнение грани ABC; 3. уравнения и длину высоты DH, опущенной из вершины D на грань ABC;
Даны координаты вершин пирамиды ABCD.
Найти:
1. уравнения ребер АВ, АС и AD;
2. уравнение грани ABC;
3. уравнения и длину высоты DH, опущенной из вершины D на грань ABC;
4. уравнение плоскости, проходящей через вершину D параллельно грани АВС.
A(3, –2, 3), B(0, 1, 2), C(5, 1, 0), D(7, 2, 8).
Геометрия
Не только решаем задачи по геометрии
Частые вопросы
Наша ИИ самая крутая и вообще первое второе третье и что-то еще в одну или две строки
Какие задачи по геометрии есть в базе Библиотеки?
Как найти нужную задачу по геометрии?
Что делать, если нужной мне задачи по геометрии нет в базе?
Как работает подписка?
Что делать, если ответ на задачу по геометрии не подойдёт?
Как быстро я получу решение задачи?