Условие:
В коробку (с крышкой), представляющую собой куб со стороной единичной длины, поместили два шара.
Каков максимальный объём, занимаемый шарами?
Каковы их радиусы?
Решить без использования производной.
Решение:
1) Очевидно, максимальный объем получим при наибольшем удалении шаров друг от друга, т. е. центры шаров должны лежать на диагонали куба.
2) Пусть R1 и R2 радиусы шаров. Поскольку шары касаются трех граней куба, то расстояния от их центров до ближайших вершин равны соответственно:
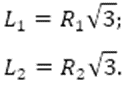
Шары касаются друг друга, поэтому расстояние между их центрами равно:
L=R1+R2
Поскольку центры шаров лежат на диагонали...