Условие:
Истечение происходит из открытого резервуара в атмосферу при постоянном напоре воды H1 по короткому трубопроводу переменного поперечного сечения с диаметрами d1 и d2 и длинами l1 и l2, для которых коэффициенты гидравлического трения соответственно равны λ1 и λ2. На втором участке трубопровода имеются два колена с плавным поворотом и понижением трубопровода на H2 = 1,5 м и задвижка, коэффициент сопротивления каждого поворота ξк, коэффициент сопротивления задвижки ξз. Истечение из конически расходящегося насадка с диаметром выходного сечения dн и длиной lн = 5dн происходит под уровень при постоянной разности уровней H. Коэффициент скорости и коэффициент расхода насадка равны φн = μн.
Определить:
1. Скорость истечения Vтр и расход Qтр через короткий трубопровод.
2. Скорость истечения Vн и расход Qн через затопленный конически расходящийся насадок.
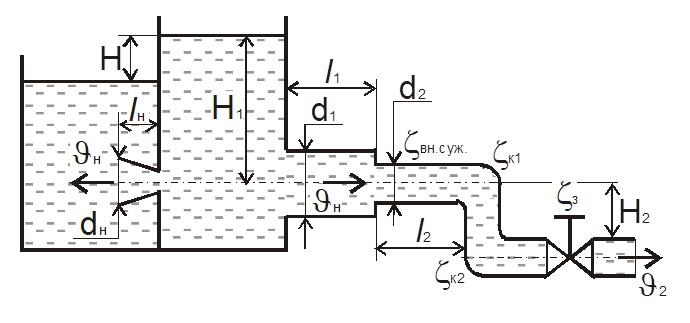
Исходные данные:
L1 = 1,2 м ; L2 = 4 м ; d1 = 0,04 м ; d2 = 0,01 м ; dH = 0,02 м ;
H = 3 м ; H1 = 9 м ; H2 = 1,5 м ; μH = 0,45 ; φH = 0,45 ;
ςB = 8 ; λ1 = 0,04 ; λ2 = 0,025 ; ς1K = 0,15 ; ς2K = 0,15 .
Решение:
1. Запишем уравнение Бернулли для сечения 1 1, проходящего по поверхности воды в резервуаре и сечения 2 2, проходящего по выходу из трубопровода; плоскость сравнения проведем по оси нижней трубы.
Получим:
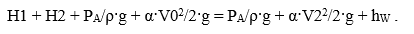
Здесь V0 = 0
