Из большого открытого резервуара А, в котором поддерживается постоянный уровень жидкости, по трубопроводу, состоящему из двух последовательно соединенных трубопроводов жидкость при температуре 20 ̊ С течет в резервуар Б.

16 марта 2025
Гидравлика

Условие:

Из большого открытого резервуара А, в котором поддерживается постоянный уровень жидкости, по трубопроводу, состоящему из двух последовательно соединенных трубопроводов жидкость при температуре 20 ̊ С течет в резервуар Б. Разность уровней жидкостей в резервуарах А и Б равна Н. Длина труб l и l₂, а их диаметры d и d₂.

Определить расход жидкости Q, протекающей по трубопроводам 1 и 2. В расчетах принять, что местные потери напора составляют 15% от потерь по длине.

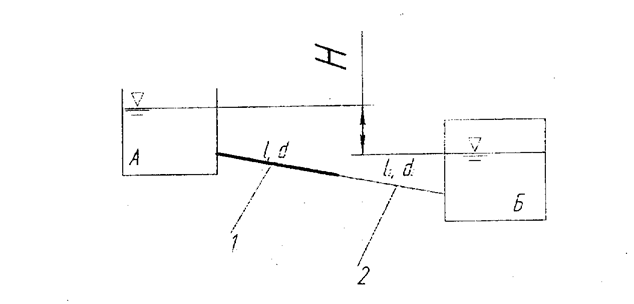
Исходные данные: жидкость – вода, Н = 7 м, l = 7,0 м,

l₂ = 8 м, d = 0,07 м, d₂ = 0,04 м

Решение:

На основании уравнения неразрывности потока расход жидкости по каждому из участков трубопровода будет одинаков. В рассматриваемом случае потери напора равны разности отметок входного и выходного сечений, Н_пот = Н. (Потери напора включают в себя потери по длине и потери в местных сопротивлениях).

Определим потери по длине:

h_l = 7 /1,15 = 6,1 м

где 1,15 - коэффициент, учитывающий местные потери (15% по условию задачи).

Потери по длине h_l = 6,1 м

В формулу для определения потерь по длине трубопровода вместо скорости подставляем выражение: