Условие:
По заданному закону движения материальной точки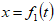 
и 
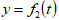найти уравнение траектории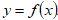 
Для момента времени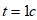 
определить:
- положение точки на траектории, проекции скорости на координатные оси и ее модуль,
- проекции ускорения на координатные и естественные оси, модуль ускорения, радиус кривизны траектории.
Результаты представить на рисунке, где необходимо нарисовать траекторию движения точки, указать точку начала движения при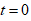 
и ее положение при 
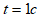, изобразить векторы скорости, ускорения и их составляющие.
Исходные данные:
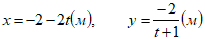(1)
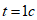
Решение:
Уравнение движения (1) можно рассматривать как параметрические уравнения траектории точки. Чтобы получить уравнения траектории в координатной форме, исключим время t из уравнений.
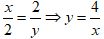
Получаем - гипербола