Пиши учебные работы
- 1. Факты из актуальных источников
- 2. Уникальность от 90% и оформление по ГОСТу
- 3. Таблицы, графики и формулы к тексту
Свыше 2 миллионов материалов для учебы
Пример задачи: «Два маленьких массивных шарика закреплены на концах невесомого стержня длины d. Стержень может вращаться в горизонтальной...»
Построить три проекции отрезка АВ, заданного координатами точек А и В. Отложить от точки А отрезок АС длиной тридцать мм
Построить три проекции отрезка АВ, заданного координатами точек А и В. Отложить от точки А отрезок АС длиной 30мм
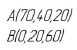
Начертательная геометрия
Показать условное изображение резьбы на стержне (М20х1,5) при длине нарезанной части L. Построить вид слева. Показать условное изображение резьбы на стержне
Показать условное изображение резьбы на стержне (М20х1,5) при длине нарезанной части L. Построить вид слева.
Начертательная геометрия
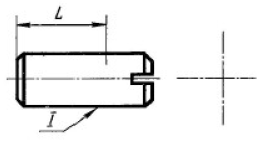
По чертежу детали сформулируйте основные требования по точности размеров, формы, взаимного расположения поверхностей и качества поверхностного слоя.
По чертежу детали сформулируйте основные требования по точности размеров, формы, взаимного расположения поверхностей и качества поверхностного слоя. Рассчитать необходимое усилие зажима на технологическую операцию по обработке отверстия Ø10Н7.
Основные требования:
1) Точности размеров: отверстие Ø6H7 выполнено по 7-му квалитету, размер толщины 16-0,1 мм выполнен с допуском 0,1 мм, отверстия Ø10H7 выполнены по 7-му квалитету. Размеры положения отверстий: 7±0,2 мм, 8±0,1 мм, 90±0,1 мм, 60±0,05 мм, 18±0,3 мм, 16±0,8 мм. Неуказанные предельные отклонения размеров по 14-му квалитету.
2) Формы: отклонения формы не заданы;
3) Взаимного расположения поверхностей: допуск перпендикулярности оси отверстия Ø6H7 относительно торца 0,06 мм, допуск зависимый; допуск перпендикулярности оси отверстия Ø10H7 относительно торца 0,06 мм, допуск зависимый; Допуск параллельности нижнего торца 0,05 мм относительно базы Б (верхний торец).
4) Шероховатости: шероховатость отверстий Ø6H7, Ø10H7 – Ra0,4 мкм. Шероховатости левого, нижнего и верхнего торцов – Ra3,2 мкм.
Неуказанная шероховатость – Ra6,3 мкм. Шероховатость образована – обработкой со снятием металла.
Начертательная геометрия
Построить линию пересечения конуса вращения с цилиндром вращения. Оси поверхностей вращения – взаимно перпендикулярные скрещивающиеся проецирующие прямые.
Построить линию пересечения конуса вращения с цилиндром вращения. Оси поверхностей вращения – взаимно перпендикулярные скрещивающиеся проецирующие прямые.
Начертательная геометрия
Вычислить площадь фигуры, ограниченной заданными линиями y=1/2, y=x, x=2. Сделаем чертеж Найдем точки пересечения тогда площадь фигуры равна
Вычислить площадь фигуры, ограниченной заданными линиями y=1/2, y=x, x=2.
Начертательная геометрия
1. Провести анализ изображения изделия, определить из каких сборочных единиц оно состоит. Представить геометрическую форму, взаимное расположение деталей, способы их соединения и взаимодействие деталей.
1. Провести анализ изображения изделия, определить из каких сборочных единиц оно состоит. Представить геометрическую форму, взаимное расположение деталей, способы их соединения и взаимодействие деталей.
2. Построить рабочие чертежи заданных деталей.
3. Построить изображение детали в аксонометрической проекции в графической среде AutoCAD.
4. Выполнить пояснительную записку.
Задание представлено на рисунке 1.1.
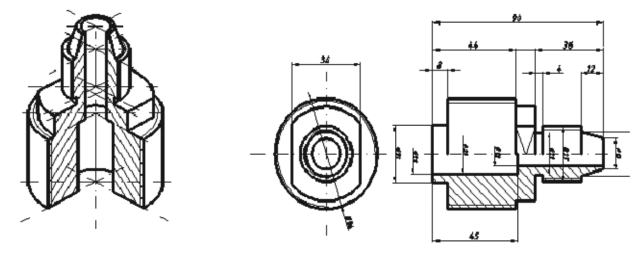
Рисунок 1.1 – Эскиз детали «Наконечник»
Начертательная геометрия
1.Прямая при прямоугольном проецировании проецируется в точку при условии... : - A. Если эта прямая проходит через центр проецирования - B. Параллельности этой прямой плоскости проекций
1.Прямая при прямоугольном проецировании проецируется в точку при условии... :
- A. Если эта прямая проходит через центр проецирования
- B. Параллельности этой прямой плоскости проекций
- C. Если эта прямая находится под углом 45° к плоскости проекций
- D. Перпендикулярности этой прямой плоскости проекций
2.Прямая при центральном проецировании проецируется в точку при условии...
- A. Если эта прямая проходит через центр проецирования
- B. Если эта прямая находится под углом 45° к плоскости проекций
- C. Перпендикулярности этой прямой плоскости проекций
- D. Параллельности этой прямой плоскости проекций
3.Проецирование называют центральным, если проецирующие лучи …
- A. Не параллельны между собой
- B. Проходят под острым углом к плоскости проекций
- C. Перпендикулярны плоскости проекций
- D. Проходят через одну точку
4.Проецирование называют ортогональным, если проецирующие лучи …
- A. Проходят через одну точку
- B. Проходят под острым углом к плоскости проекций
- C. Не параллельны между собой
- D. Перпендикулярны плоскости проекций
5.Плоскость проекций, обозначаемая на чертеже H , называется…
- A. Фронтальной плоскостью проекций
- B. Горизонтальной плоскостью проекций
- C. Профильной плоскостью проекций
6.Проецирование называют ортогональным, если проецирующие лучи …
- A. Проходят через одну точку
- B. Параллельны между собой и перпендикулярны по отношению к плоскости проекций
- C. Параллельны между собой
7.При центральном проецировании сохраняется…
- A. Натуральная величина отрезка прямой
- B. Перпендикулярность отрезков прямых
- C. Принадлежность точки прямой
- D. Параллельность отрезков прямых
8.Какое из сформулированных предложений отношений принадлежности евклидова пространства означает - необходимы две точки, чтобы провести одну прямую?
- A. Если точка принадлежит прямой, а прямая принадлежит плоскости, то точка принадлежит плоскости.
- B. Три различные точки A, B и C, не принадлежащие одной прямой, принадлежат одной и той же и только одной плоскости.
- C. Если две точки, принадлежащие прямой, принадлежат плоскости то и прямая принадлежит плоскости.
- D. Две различные точки всегда принадлежат одной и той же и только одной прямой или каждой прямой принадлежат, по крайней мере, две точки.
9.Преобразование пространственного макета в эпюр осуществляется ...
- A. поочередным совмещением плоскостей W и H с фронтальной плоскостью проекций V. Для совмещения W поворачиваем на 90° вокруг оси z в направлении движения часовой стрелки и H поворачиваем на 90° вокруг оси z в направлении против движения часовой стрелки.
- B. поочередным совмещением плоскостей H и W с фронтальной плоскостью проекций V. Для совмещения H поворачиваем на 90° вокруг оси x в направлении движения часовой стрелки и W поворачиваем на 90° вокруг оси z в направлении против движения часовой стрелки.
- C. поочередным совмещением плоскостей W и H с фронтальной плоскостью проекций V. Для совмещения W поворачиваем на 90° вокруг оси z в направлении против движения часовой стрелки и H поворачиваем на 90° вокруг оси z в направлении движения часовой стрелки.
- D. поочередным совмещением плоскостей H и W с фронтальной плоскостью проекций V. Для совмещения H поворачиваем на 90° вокруг оси x в направлении против движения часовой стрелки и W поворачиваем на 90° вокруг оси z в направлении против движения часовой стрелки.
10.Какой из способов проецирования обладает следующими преимуществами перед другими?: - простота геометрических построений для определения проекций точек; - Возможность при определенных условиях сохранить на проекциях форму и размеры проецируемой фигуры.
- A. Прямоугольное проецирование
- B. Центральное проецирование
- C. Косоугольное проецирование
11.Плоскость, на которой получают изображение геометрического объекта, называют...
- A. плоскостью изображений
- B. плоскостью проекций
- C. плоскостью отображений
- D. плоскостью чертежа
12.Положение точки на чертеже однозначно определяется как минимум … проекциями
- A. четырьмя
- B. пятью
- C. двумя
- D. тремя
13.Проекция точки определяется соответствующими координатами X, Y, Z. Горизонтальная проекция точки определяется ...
- A. X, Y
- B. X, Z
- C. Y, Z
14.Проекция точки определяется соответствующими координатами X, Y, Z. Фронтальная проекция точки определяется ...
- A. X, Y
- B. X, Z
- C. Y, Z
15.Проекция точки определяется соответствующими координатами X, Y, Z. Профильная проекция точки определяется ...
- A. Y, Z
- B. X, Y
- C. X, Z
16.Линия, соединяющая на чертеже проекции точки и перпендикулярная к оси проекций, называется…
A. линией уровня
B. постоянной чертежа
C. линией проекционной связи
D. связующей прямой
17.Из заданных точек: D (6,5,5); B (12,6,12); A (12,15,15); E (18,17,18); C (9,9,4)
От фронтальной и профильной плоскостей проекций равно удалена точка ...
18.Из заданных точек: D (6,5,5); B (12,6,12); A (12,15,15); E (18,17,18); C (9,9,4)
От профильной плоскости проекций равно удалены точки ...
19.Из заданных точек: D (6,5,5); B (12,6,12); A (12,15,15); E (18,17,18); C (9,9,4)
От горизонтальной плоскости проекций больше всех удалена точка ...
20.Из заданных точек: D (6,5,5); B (12,6,12); A (12,15,15); E (18,17,18); C (9,9,4)
Ближе всех к профильной плоскости проекций точка ...
21.Из заданных точек: D (6,5,5); B (12,6,12); A (12,15,15); E (18,17,18); C (9,9,4)
От фронтальной и горизонтальной плоскостей проекций равно удалены точки ...
22.Из заданных точек: D (6,5,5); B (12,6,12); A (12,15,15); E (18,17,18); C (9,9,4)
От горизонтальной и профильной плоскостей проекций равно удалены точки ...
23.Из заданных точек: D (6,5,5); B (12,6,12); A (12,15,15); E (18,17,18); C (9,9,4)
Самая низкая точка ...
24.Из заданных точек: D (6,5,5); B (12,6,12); A (12,15,15); E (18,17,18); C (9,9,4)
Самая высокая точка ...
25.Проекция точки на плоскость проекций H называется…
A. фронтальной
B. горизонтальной
C. профильной
26.Проекция точки на плоскость проекций V называется…
B. горизонтальной
C. профильной
A. фронтальной
27.Проекция точки на плоскость проекций W называется…
B. горизонтальной
C. профильной
A. фронтальной
28.Плоскость на чертеже можно задать...
A. проекциями параллельных прямых
B. проекциями пересекающихся прямых
C. проекциями скрещивающихся прямых
D. проекциями треугольника
29.Минимальное количество геометрических объектов для задания плоскости:
A. три точки не лежащие на одной прямой
B. одна прямая
C. пять прямых
D. две пересекающиеся прямые
30.Плоскость на чертеже не задают…
A. три точки
B. точка и прямая
C. две параллельные прямые
D. две пересекающиеся прямые
E. две скрещивающиеся прямые
31.Отрезок прямой АВ, если А(10,10,30) и В(10,10,50), расположен в пространстве…
A. перпендикулярно профильной плоскости проекций
B. перпендикулярно горизонтальной плоскости проекций
C. параллельно биссекторной плоскости
D. параллельно горизонтальной плоскости проекций
Начертательная геометрия
1 Постройте фронтальную проекцию линии n, лежащей на конической поверхности Σ(S,v). 2 Построить следы плоскости, заданной двумя пересекающимися прямыми АВ и СD.
1 Постройте фронтальную проекцию линии n, лежащей на конической поверхности Σ(S,v).
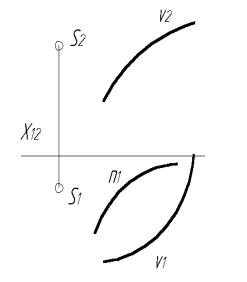
2 Построить следы плоскости, заданной двумя пересекающимися прямыми АВ и СD.
3 Построить точку пересечения прямой а с плоскостью Г и определить видимость прямой по отношению к плоскости.
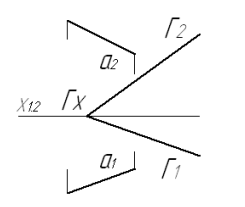
Начертательная геометрия
Проекционное черчение. Даны две проекции детали. Требуется построить третий вид детали, выполнить необходимые разрезы и сечения.
Проекционное черчение.
Даны две проекции детали.
Требуется построить третий вид детали, выполнить необходимые разрезы и сечения.
Все построения производились согласно ЕСКД (единой системы конструкторской документации).
Формат выбран по ГОСТ 2.301
Масштаб выбран 1:1 согласно ГОСТ 2.302
Разрезы и сечение выполнены согласно ГОСТ2.305
Размеры проставлены согласно ГОСТ 2.307
Графическое обозначение разрезов – по ГОСТ 2.306 (выбрано обозначение материала – металл)
Основная надпись чертежа выполнена по ГОСТ 2.104
Начертательная геометрия
Ответить письменно на вопросы: 1. Какая прямая называется прямой общего положения, как располагаются ее проекции? 2. Какие прямые называются прямыми уровня, проецирующими?
Ответить письменно на вопросы:
1. Какая прямая называется прямой общего положения, как располагаются ее проекции?
2. Какие прямые называются прямыми уровня, проецирующими?
3. Что называется следами прямой линии?
4. Каким может быть взаимное положение прямых?
5. Какие точки называются конкурирующими, для чего их используют?
Начертательная геометрия
Найти площадь фигуры, ограниченной линиями: r=6sin𝜑 r=4sin𝜑 Построим область, ограниченную окружностями r=6sin𝜑, r=4sin𝜑
Найти площадь фигуры, ограниченной линиями:
r=6sin𝜑
r=4sin𝜑
Начертательная геометрия
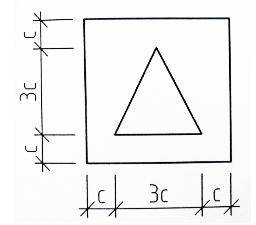
Геометрические характеристики плоских сечений. Для заданных плоских сечений требуется: 1. Определить положение центра тяжести сечения;
Геометрические характеристики плоских сечений.
Для заданных плоских сечений требуется:
1. Определить положение центра тяжести сечения;
2. Вычислить осевые и центробежный моменты инерции относительно центральных осей;
3. Определить положение главных центральных осей и вычислить моменты инерции, моменты сопротивления и радиусы инерции относительно этих осей;
4. Вычертить сечения в масштабе 1:1, 1:2, 1:5 и показать все необходимые при расчёте обозначения и положение главных осей инерции.
Заданная схема:
Начертательная геометрия
Геометрические характеристики плоских сечений Для заданного плоского сечения определить положение главных центральных осей и вычислить основные
Геометрические характеристики плоских сечений
Для заданного плоского сечения определить положение главных центральных осей и вычислить основные геометрические характеристики.
Порядок выполнения работы:
1. Вычертить сечение в масштабе, указать размеры.
2. Определить положение центра тяжести сечения.
3. Вычислить моменты инерции относительно центральных осей.
4. Определить положение главных центральных осей и величину главных центральных моментов инерции.
5. Вычислить моменты сопротивления относительно главных центральных осей и главные радиусы инерции.
Исходные данные: швеллер №18a, уголок 100x63x10.
Начертательная геометрия
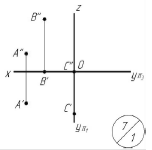
По двум заданным проекциям точек А,B,C построить третью. По двум заданным проекциям точек А,B,C построить третью. Построить наглядные изображения точек.
По двум заданным проекциям точек А,B,C построить третью.
Построить наглядные изображения точек.
Начертательная геометрия
Определение центра тяжести плоских фигур Цель работы – определить центр тяжести сложной фигуры аналитическим путем. Начертим фигуру в масштабе, разобьём ее на простейшие элементы и проставим размеры.
Определение центра тяжести плоских фигур
Цель работы – определить центр тяжести сложной фигуры аналитическим путем.4
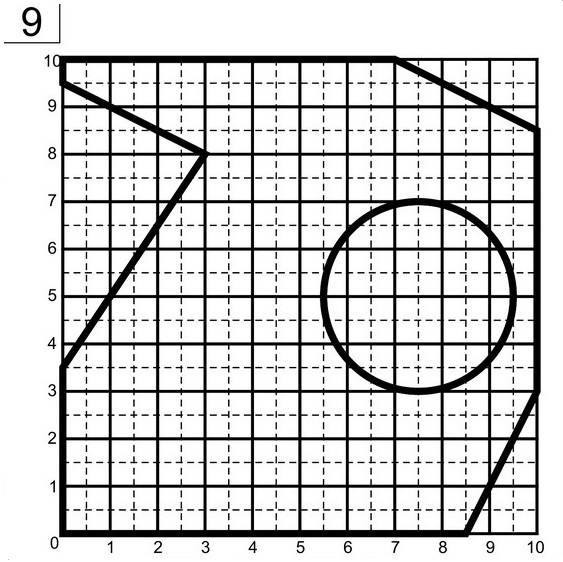
Рис. 1
Начертательная геометрия
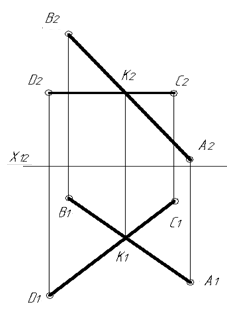
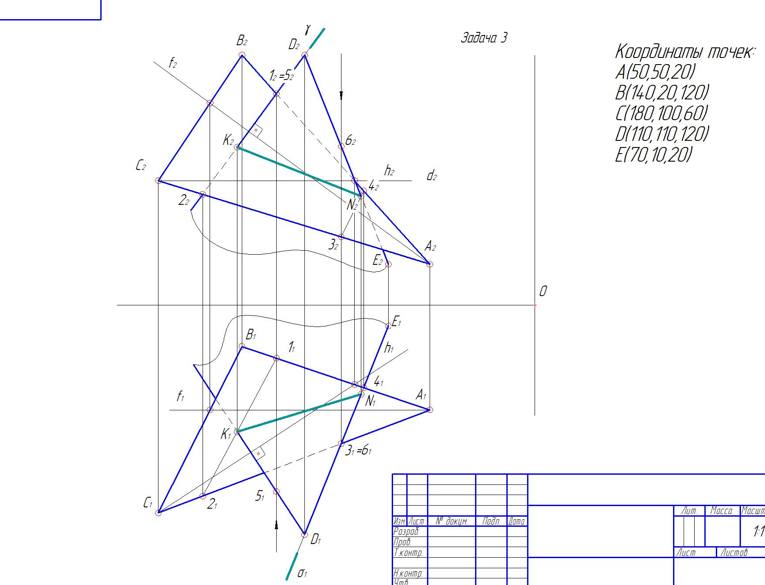
Через прямую DE провести плоскость, перпендикулярную плоскости, заданной треугольником ABC. построить линию пересечения этих двух плоскостей,
Через прямую DE провести плоскость, перпендикулярную плоскости ![]() , заданной треугольником ABC. построить линию пересечения этих двух плоскостей, определить видимость
, заданной треугольником ABC. построить линию пересечения этих двух плоскостей, определить видимость
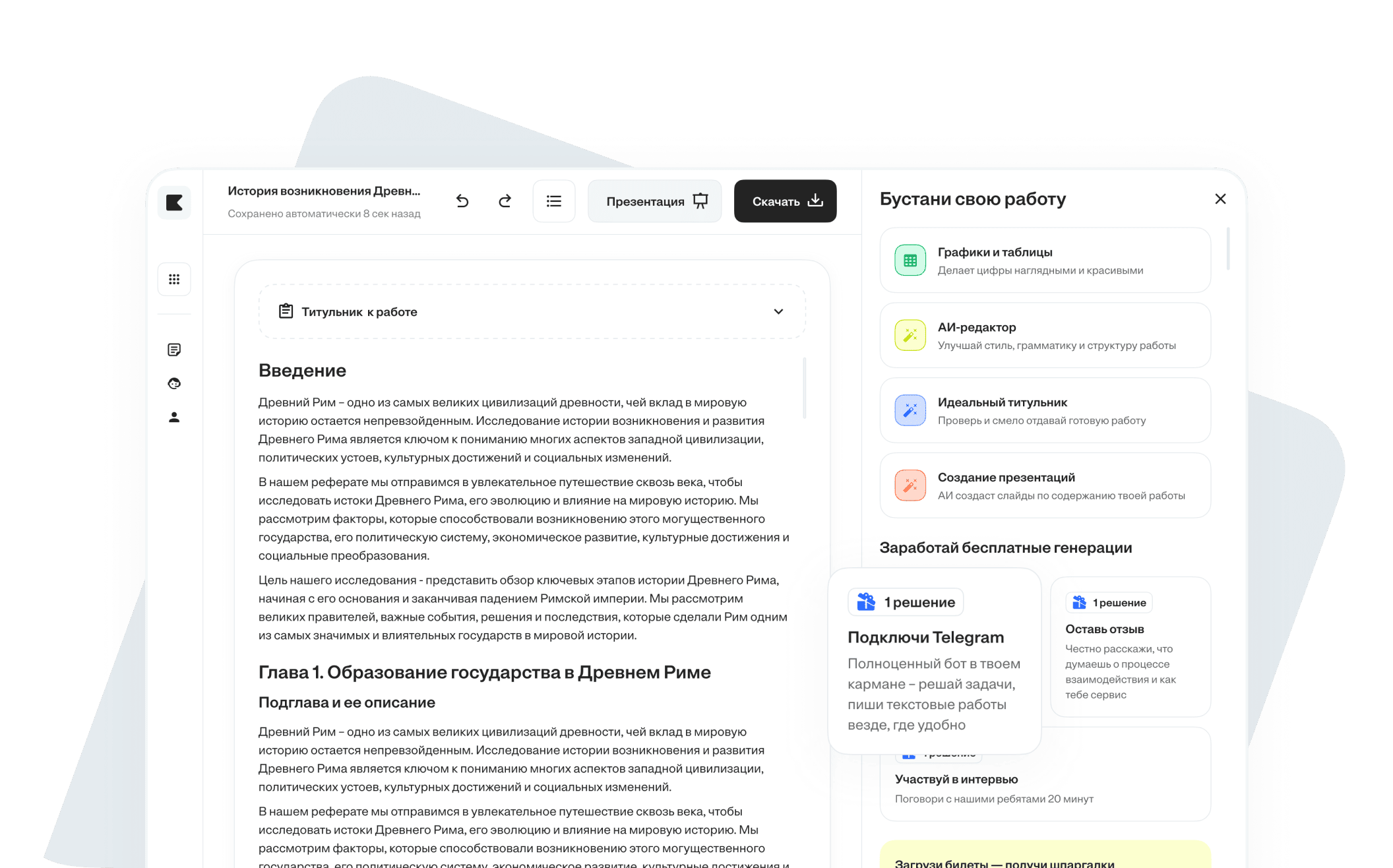
Точки A, B, C ,D и E имеют следующие координаты:
A (170, 120 ,80)
B (140, 45, 135)
C (70, 50, 60)
D (185, 45, 55)
E(60,70,75
Начертательная геометрия
Построить горизонтальную проекцию правильной пятигранной усеченной пирамиды. Пересекая многогранник плоскостью, в сечении имеем плоский многоугольник с вершинами и сторонами
Построить горизонтальную проекцию правильной пятигранной усеченной пирамиды. Рис. 16
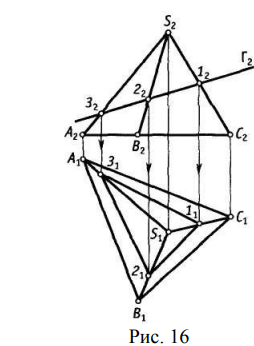
Начертательная геометрия
Тонкими линиями на листах подготовленных форматов начертить три проекции каждой поверхности в соответствии с масштабом; Вычертить заданные проекции сквозных вырезов на фронтальных проекциях поверхностей;
Тонкими линиями на листах подготовленных форматов начертить три проекции каждой поверхности в соответствии с масштабом;
Вычертить заданные проекции сквозных вырезов на фронтальных проекциях поверхностей;
Используя условия принадлежности точки и линии поверхности, построить недостающие проекции этих вырезов.
Начертательная геометрия
На листе формата А3 начертить в трех проекциях чертеж, аксонометрическую (изометрическую) проекцию и развертку тела вращения (цилиндра), усеченного проецирующей плоскостью.
На листе формата А3 начертить в трех проекциях чертеж, аксонометрическую (изометрическую) проекцию и развертку тела вращения (цилиндра), усеченного проецирующей плоскостью.
Начертательная геометрия
«Сечение пирамиды плоскостью» Построим 3 проекции пирамиды DABC и фронтальную проекцию вырожденной треугольной призмы. В пирамиде от призмы образовано окно
«Сечение пирамиды плоскостью»
Построить линию взаимного пересечения двух многогранников (пирамида с призматическим отверстием), определить видимость этой линии и других элементов многогранников.
Определить н.в. фигуру заданного сечения.
Начертательная геометрия
Опишите прямые и плоскости, изображенные на рисунке. 1-Прямая уровня. Фронталь. Она расположена параллельно фронтальной плоскости. Ее горизонтальная проекция параллельна оси Х.
Дайте описание прямых и плоскостей, изображенных на рисунке.
Начертательная геометрия
Дан квадрат ABCD. Точка О – точка пересечения диагоналей. На стороне АВ квадрата ABCD построен равнобедренный треугольник ABК, в котором КА=КВ. Точка К расположена вне квадрата, точка L – середина АК, точка М – точка пересечения отрезков LO и KD.
Дан квадрат ABCD. Точка О – точка пересечения диагоналей. На стороне АВ квадрата ABCD построен равнобедренный треугольник ABК, в котором КА=КВ. Точка К расположена вне квадрата, точка L – середина АК, точка М – точка пересечения отрезков LO и KD.
Доказать, что треугольник МКО – равнобедренный.
Начертательная геометрия

Из всех нейронок именно он идеально подходит для студентов. на любой запрос дает четкий ответ без обобщения.

Очень хорошо подходит для брейншторма. Все идет беру с этого сайта. Облегчает работу с исследовательскими проектами
Очень помогло и спасло меня в последние дни перед сдачей курсовой работы легкий,удобный,практичный лучше сайта с подобными функциями и материалом не найти!

Обучение с Кампус Хаб — очень экономит время с возможностю узнать много новой и полезной информации. Рекомендую ...
Пользуюсь сайтом Кампус АИ уже несколько месяцев и хочу отметить высокий уровень удобства и информативности. Платформа отлично подходит как для самостоятельного обучения, так и для профессионального развития — материалы структурированы, подача информации понятная, много практики и актуальных примеров.

Хочу выразить искреннюю благодарность образовательной платформе за её невероятную помощь в учебе! Благодаря удобному и интуитивно понятному интерфейсу студенты могут быстро и просто справляться со всеми учебными задачами. Платформа позволяет легко решать сложные задачи и выполнять разнообразные задания, что значительно экономит время и повышает эффективность обучения. Особенно ценю наличие подробных объяснений и разнообразных материалов, которые помогают лучше усвоить материал. Рекомендую эту платформу всем, кто хочет учиться с удовольствием и достигать отличных результатов!

Для студентов просто класс! Здесь можно проверить себя и узнать что-то новое для себя. Рекомендую к использованию.
Как студент, я постоянно сталкиваюсь с различными учебными задачами, и эта платформа стала для меня настоящим спасением. Конечно, стоит перепроверять написанное ИИ, однако данная платформа облегчает процесс подготовки (составление того же плана, содержание работы). Также преимущество состоит в том, что имеется возможность загрузить свои источники.

Сайт отлично выполняет все требования современного студента, как спасательная волшебная палочка. легко находит нужную информацию, совмещает в себе удобный интерфейс и качественную работу с текстом. Грамотный и точный помощник в учебном процессе. Современные проблемы требуют современных решений !!
Здесь собраны полезные материалы, удобные инструменты для учёбы и актуальные новости из мира образования. Интерфейс интуитивно понятный, всё легко находить. Особенно радует раздел с учебными пособиями и лайфхаками для студентов – реально помогает в учёбе!

Я использовала сайт для проверки своих знаний после выполнения практических заданий и для поиска дополнительной информации по сложным темам. В целом, я осталась довольна функциональностью сайта и скоростью получения необходимой информации
Хорошая нейросеть,которая помогла систематизировать и более глубоко проанализировать вопросы для курсовой работы.

Кампус АИ — отличный ресурс для тех, кто хочет развиваться в сфере искусственного интеллекта. Здесь удобно учиться, есть много полезных материалов и поддержки.
Больше отзывов
Какие задачи по начертательной геометрии есть в базе Библиотеки?
Как найти нужную задачу по начертательной геометрии?
Что делать, если нужной мне задачи по начертательной геометрии нет в базе?
Как работает подписка?
Что делать, если ответ на задачу по начертательной геометрии не подойдёт?
Как быстро я получу решение задачи?