Бросаем неправильную игральную кость. На ее гранях написано три раза 5, два раза 7 и одни раз 1. Написать закон распределения случайного числа Z, равного количеству выпадения числа 5 при трех бросаниях.
«Бросаем неправильную игральную кость. На ее гранях написано три раза 5, два раза 7 и одни раз 1. Написать закон распределения случайного числа Z, равного количеству выпадения числа 5 при трех бросаниях.»
- Теория вероятностей
Условие:
Бросаем неправильную игральную кость. На ее гранях написано три раза 5, два раза 7 и одни раз 1. Написать закон распределения случайного числа Z, равного количеству выпадения числа 5 при трех бросаниях. Вычислить M(Z), D(Z), написать функцию распределения F(x): вычислить вероятности событий Z ∈ [-2; 1; 3], Z ∈ [3; 8].
Решение:
Вероятность выпадения числа 5 на такой неправильной игральной кости равна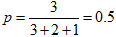 
. В качестве случайной величины в данной задаче выступает числа выпадения числа 5 при трех бросаниях. Обозначим ее через Z.
Перечислим все возможные значения случайной величины Z : 0, 1, 2, 3.
Вероятность того, что выпадет число 5 - постоянна и равна 0,5 (p =0,5). Вероятность противоположного события, т.е. того, что число 5 не...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э