Условие:
Функция распределения непрерывной случайной величины задана выражением:
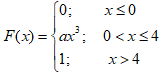
Найти величину коэффициента 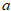 , написать аналитическое выражение и простроить график плотности распределения вероятностей, найти математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины. Найти вероятности попадания данной случайной величины в интервалы
, написать аналитическое выражение и простроить график плотности распределения вероятностей, найти математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины. Найти вероятности попадания данной случайной величины в интервалы 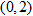 и
и 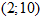 .
.
Решение:
Параметр 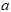 определим из непрерывности функции распределения, то
определим из непрерывности функции распределения, то
есть 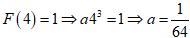 , то есть
, то есть
