База задач по теории вероятностей
Свыше 2 миллионов материалов для учебы
Пример задачи: «Два маленьких массивных шарика закреплены на концах невесомого стержня длины d. Стержень может вращаться в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня...»
- Материалы со всех ВУЗов страны
- Примеры, чтобы разобраться
- 160+ дисциплин в базе
- 2 000 000+ решенных задач
Список решенных задач
Сборщик получил 4 коробки деталей изготовленных заводом №1 и 6 коробок деталей, изготовленных заводом №2. Вероятность того, что деталь завода №1 высшего качества, равна 0,9, а для завода №2 такая вероятность равна 0,8. Найти вероятность того, что взятая
Сборщик получил 4 коробки деталей изготовленных заводом №1 и 6 коробок деталей, изготовленных заводом №2. Вероятность того, что деталь завода №1 высшего качества, равна 0,9, а для завода №2 такая вероятность равна 0,8. Найти вероятность того, что взятая наугад деталь будет высшего качества.
Теория вероятностей
Игральный кубик бросают два раза. Найти вероятность того, что сумма выпавших очков будет равна 8. Игральный кубик имеет 6 граней с цифрами от 1 до 6. Вероятность того, что на верхней грани кубика появится заданная цифра рана 1/6 и не зависит от
Игральный кубик бросают два раза. Найти вероятность того, что сумма выпавших очков будет равна 8.
Теория вероятностей
Независимые случайные величины X, Y могут принимать только целые значения: Y – от 1 до 15 c вероятностью 1/15, а X только значения 6 и 9, при этом P (X = 6) = 9/10.
Независимые случайные величины X, Y могут принимать только целые значения: Y – от 1 до 15 c вероятностью 1/15, а X только значения 6 и 9, при этом P (X = 6) = 9/10.
Найдите вероятность того, что сумма данных случайных величин будет меньше 15.
Теория вероятностей
В коробке находится 6 синих, 8 красных и 11 зеленых карандашей. Одновременно вынимают 21 карандаш. Найти вероятность того, что среди них будет 5 синих и 6 красных карандашей.
В коробке находится 6 синих, 8 красных и 11 зеленых карандашей. Одновременно вынимают 21 карандаш. Найти вероятность того, что среди них будет 5 синих и 6 красных карандашей.
Теория вероятностей
Аудитория освещается двумя лампами. Вероятность перегорания лампы в течение года равна 0,3. Найти вероятность того, что в течение года хотя бы одна лампа не перегорит.
Аудитория освещается двумя лампами. Вероятность перегорания лампы в течение года равна 0,3. Найти вероятность того, что в течение года хотя бы одна лампа не перегорит.
Теория вероятностей
Научная конференция проводится в 3 дня. Всего запланировано 70 докладов – в первый день 20 докладов, остальные распределены поровну между вторым и третьим днями.
Научная конференция проводится в 3 дня. Всего запланировано 70 докладов – в первый день 20 докладов, остальные распределены поровну между вторым и третьим днями. Порядок докладов определяется жеребьёвкой.
Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Теория вероятностей
На конференцию приехали 3 ученых из Норвегии, 3 из России, 4 из Испании. Каждый из них делает на конференции один доклад. Порядок докладов определяется жеребьевкой.
На конференцию приехали 3 ученых из Норвегии, 3 из России, 4 из Испании. Каждый из них делает на конференции один доклад. Порядок докладов определяется жеребьевкой.
Найдите вероятность того, что восьмым окажется доклад ученого из России
Теория вероятностей
Система состоит из пяти приборов, средняя наработка до первого отказа которых равна: T_1=83 ч,T_2=220 ч, T_3=280 ч,T_4=400 ч,T_5=700 ч. Для приборов справедлив экспоненциальный закон надежности. Требуется найти среднюю наработку до первого отказа
Система состоит из пяти приборов, средняя наработка до первого отказа которых равна:
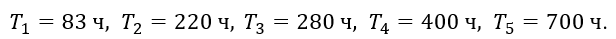 . Для приборов справедлив экспоненциальный закон надежности. Требуется найти среднюю наработку до первого отказа системы.
. Для приборов справедлив экспоненциальный закон надежности. Требуется найти среднюю наработку до первого отказа системы. Теория вероятностей
В равносторонний треугольник, длина стороны которого равна , наудачу бросается точка. Вероятность попадания точки одинакова по всей площади треугольника.
В равносторонний треугольник, длина стороны которого равна а, наудачу бросается точка. Вероятность попадания точки одинакова по всей площади треугольника. В треугольник вписана окружность, в эту окружность вписан квадрат.
Какова вероятность того, что наудачу брошенная в треугольник точка попала в окружность, но не попала в квадрат?
Теория вероятностей
Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу извлеченный кубик имеет три окрашенные грани.
Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера, которые затем тщательно перемешаны.
Найти вероятность того, что наудачу извлеченный кубик имеет три окрашенные грани.
Теория вероятностей
Дана выборка значений нормально распределенного признака Х ( в первой строке указаны значения признака , во второй - соответствующие им частоты ). Найти : 1) выборочную среднюю
Дана выборка значений нормально распределенного признака Х ( в первой строке указаны значения признака xi, во второй - соответствующие им частоты ni).
Найти :
1) выборочную среднюю
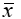 и исправленное среднее квадратичное отклонение s методом произведений;
и исправленное среднее квадратичное отклонение s методом произведений; 2) доверительный интервал, покрывающий с надежностью 0,95 неизвестное математическое ожидание α признака Х;
3) доверительный интервал, покрывающий неизвестное среднее квадратическое отклонение σ признака Х ( надежность оценки во всех вариантах считать равной
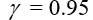 ).
). 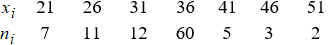
Теория вероятностей
По заданному закону распределения дискретной случайной величины Х требуется найти: математическое ожидание; дисперсию; среднее квадратическое отклонение. Построить график закона распределения – многоугольник распределения.
По заданному закону распределения дискретной случайной величины Х требуется найти: математическое ожидание; дисперсию; среднее квадратическое отклонение. Построить график закона распределения – многоугольник распределения.

Теория вероятностей
В классе 35 учеников. 20 человек посещают математический кружок, 11 – биологический. 10 человек не посещают кружков. Сколько биологов увлекается математикой?
В классе 35 учеников. 20 человек посещают математический кружок, 11 – биологический. 10 человек не посещают кружков. Сколько биологов увлекается математикой?
Теория вероятностей
На отдельных карточках написаны цифры 1, 2, 3, 4, 5, 6, 7, 8, 9. Все 9 карточек тщательно перемешаны, после чего наугад берут 4 из них и выкладывают в ряд друг за другом в порядке появления.
На отдельных карточках написаны цифры 1, 2, 3, 4, 5, 6, 7, 8, 9. Все 9 карточек тщательно перемешаны, после чего наугад берут 4 из них и выкладывают в ряд друг за другом в порядке появления.
Какова вероятность получить при этом: а) чётное число; б) число 1234?
Теория вероятностей
Три сотрудника могут составить один и тот же документ. Вероятность представить готовый документ без ошибок для них соответственно равны p1=0,5, p2=0,9, p3=0,6.
Три сотрудника могут составить один и тот же документ. Вероятность представить готовый документ без ошибок для них соответственно равны p1=0,5, p2=0,9, p3=0,6.
Составить закон распределения случайной величины X – числа готовых документов без ошибок, найти её математическое ожидание, дисперсию и среднее квадратическое отклонение.
Теория вероятностей
Вероятности четырех независимых в совокупности событий A1, A2, A3, A4 соответственно равны P( A1 ) = 0,1; P( A2 ) = 0,2; P( A3 ) = 0,3 и P( A4 ) = 0,4 . События B1 и B2 заданы с помощью словесного описания. Используя операции алгебры событий, выразите
Вероятности четырех независимых в совокупности событий A1, A2, A3, A4 соответственно равны P( A1 ) = 0,1; P( A2 ) = 0,2; P( A3 ) = 0,3 и P( A4 ) = 0,4 . События B1 и B2 заданы с помощью словесного описания. Используя операции алгебры событий, выразите события B1 и B2 через A1, A2, A3, A4. Найдите вероятности событий B1 и B2.

Теория вероятностей
Коробки с конфетами упаковываются автоматически. Их средняя масса равна 540 г. Известно, что 5% коробок имеют массу, меньшую 500 г. Каков процент коробок, масса которых от 500 до 550 г.
Коробки с конфетами упаковываются автоматически. Их средняя масса равна 540 г. Известно, что 5% коробок имеют массу, меньшую 500 г. Каков процент коробок, масса которых от 500 до 550 г.
Теория вероятностей
Три стрелка в одинаковых и независимых условиях произвели по одному выстрелу по одной и той же цели. Вероятность поражения цели первым стрелком равна
Три стрелка в одинаковых и независимых условиях произвели по одному выстрелу по одной и той же цели. Вероятность поражения цели первым стрелком равна
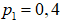 , вторым –
, вторым – 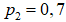 , третьим –
, третьим – 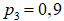 .
.Найти вероятность того, что: а) только два стрелка попали в цель; б) все три стрелка попали в цель.
Теория вероятностей
В кармане лежало 10 монет, причем у двух из них герб с обеих сторон. Наудачу взятая монета подбрасывается 3 раза. Найти вероятность того, что трижды выпадет герб.
В кармане лежало 10 монет, причем у двух из них герб с обеих сторон. Наудачу взятая монета подбрасывается 3 раза. Найти вероятность того, что трижды выпадет герб.
Теория вероятностей
Кубик подбрасывается 24 раза. Пусть Y – сумма выпавших очков. Оцените вероятности: Обозначим через число очков при ом подбрасывании кубика. Поскольку случайные величины
Кубик подбрасывается 24 раза. Пусть Y – сумма выпавших очков. Оцените вероятности:
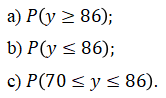
Теория вероятностей
Из 25 контрольных работ, среди которых 5 оценены на «отлично» наугад извлекаются 3 работы. Найти закон распределения дискретной случайной величины X – числа работ, оцененных на «отлично» среди извлеченных. Найти числовые характеристики
Из 25 контрольных работ, среди которых 5 оценены на «отлично» наугад извлекаются 3 работы. Найти закон распределения дискретной случайной величины X – числа работ, оцененных на «отлично» среди извлеченных. Найти числовые характеристики случайной величиныX. Построить функцию распределения
Теория вероятностей
В первой урне – 7 белых и 3 черных шара; во второй урне – 5 белых и 5 черных шаров. Из каждой урны наудачу извлекли по одному шару. Какова вероятность того, что:
В первой урне – 7 белых и 3 черных шара; во второй урне – 5 белых и 5 черных шаров. Из каждой урны наудачу извлекли по одному шару. Какова вероятность того, что:
а) оба извлеченные шары белые?
б) оба извлеченные шары черные?
в) один извлеченный шар белый, а другой − черный?
Теория вероятностей
В урне находится 5 белых, 4 черных и 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его в урну. Найти вероятность того, что при первом испытании появится белый шар, при втором черный и при третьем – синий.
В урне находится 5 белых, 4 черных и 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его в урну.
Найти вероятность того, что при первом испытании появится белый шар, при втором черный и при третьем – синий.
Теория вероятностей
Случайная величина X подчинена закону Пуассона с математическим ожиданием а= 3. Найти: а) вероятность того, что случайная величина X примет значение меньшее, чем ее математическое ожидание;
Случайная величина X подчинена закону Пуассона с математическим ожиданием а= 3.
Найти:
а) вероятность того, что случайная величина X примет значение меньшее, чем ее математическое ожидание;
б) вероятность того, что величина X примет положительное значение.
Теория вероятностей
Не только решаем задачи по теории вероятностей
Частые вопросы
Наша ИИ самая крутая и вообще первое второе третье и что-то еще в одну или две строки
Какие задачи по теории вероятностей есть в базе Библиотеки?
Как найти нужную задачу по теории вероятностей?
Что делать, если нужной мне задачи по теории вероятностей нет в базе?
Как работает подписка?
Что делать, если ответ на задачу по теории вероятностей не подойдёт?
Как быстро я получу решение задачи?