«Расчет определенного интеграла методом Монте-Карло» 1. Разработка Генератора случайных чисел (ГСЧ) равномерного закона распределения с заданными границами интегрирования на основе чисел, имеющих равномерное распределение на интервале [0,1]
- Теория вероятностей
Условие:
Выполнить лабораторную работу:
«Расчет определенного интеграла методом Монте-Карло»
1. Разработка Генератора случайных чисел (ГСЧ) равномерного закона распределения с заданными границами интегрирования на основе чисел, имеющих равномерное распределение на интервале [0,1] (Возможно использование стандартной функции).
2. Получение N ~10000 пар случайных чисел и их использование для расчета значения площади подынтегральной функции на основе метода Монте-Карло. По Х генерация чисел осуществляется в пределах интеграла, а по У – в пределах от 0 до значения F(Хмах).
3. Общая площадь рассчитывается исходя из отношения Sм-к = S*Nпоп/N, где S- площадь прямоугольника, ограничивающая подынтегральную функцию.
4. Расчет теоретического значения интеграла с заданной функцией. Оценка относительной погрешности полученного методом Монте-Карло значения площади подынтегральной функции. ((Sт – Sм-к)/ Sт).
Выводы о возможности использования метода Монте-Карло для расчета площадей.
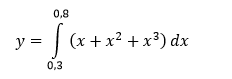
Решение:
Ход работы
Вычислим теоретическое значение интеграла:
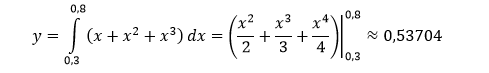
Для вычисления для расчета значения площади подынтегральной функции на основе метода Монте-Карло получим N ~10000 пар случайных чисел: по Х генерация чисел осуществляется в пределах (0,3;0,8), а по У в пределах от 0...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства