Условие:
Случайная величина X имеет нормальное распределение с параметрами M(X) и σ(X).
M(X)=25, σ(X)=4, α=13, β=30, δ=0,1
Требуется:
- Составить функцию плотности распределения и построить ее график.
- Найти вероятность того, что случайная величина в результате испытания примет значение, принадлежащее интервалу (α,β).
- Найти вероятность того, что абсолютная величина отклонения значений случайной величины от ее математического ожидания не превысит δ.
Решение:
Так как непрерывная случайная величина распределена по нормальному закону, плотность ее распределения вероятности выражается формулой:
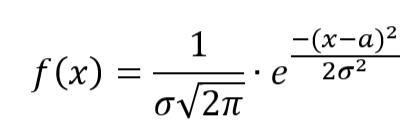
С учетом заданных параметров распределения (M(X)=a=25,(...
