Условие:
В случайные моменты времени, определяемые простейшим потоком событий интенсивности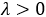 
, частица совершает случайное блуждание в пространстве, перемещаясь по узлам решетки 
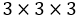узла с единичным расстоянием между соседними узлами на один шаг в один из ближайших узлов с одинаковой вероятностью. Найти предельные вероятности положений частицы. Найти предельное математическое ожидание расстояния от частицы до центральной точки решетки через бесконечно большой промежуток времени.
Решение:
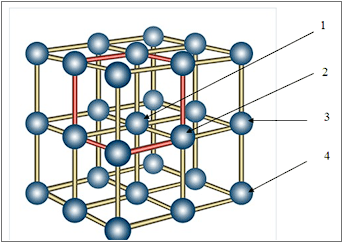
Рассмотрим поведение частицы задачу как непрерывную цепь Маркова со следующими состояниями:
- 1 частица в центре решетки;
- 2 частица в центральных узлах плоскостей (исключая центр решетки), таковых узлов шесть;
- 3 частица в узлах по периметру куба, но не в самых угловых узлах, таковых узлов двенадцать;
- 4 частица в угловых узлах, таковых узлов восемь.
Определим интенсивности переходов между сос...