Условие:
Вероятность выпуска бракованного изделия составляет ((m +1)/100)=0,02. Какова вероятность того, что среди ((n +1)×500)=1000 отобранных изделий:
а) не более (n +10)=11 изделий окажется бракованных?
б) количество бракованных изделий будет от (n +10)=11 до (n + 50)=51?
Решение:
а)
А среди 1000 отобранных изделий окажется не более 11 изделий бракованных.
Воспользуемся интегральной теоремой Муавра-Лапласа:
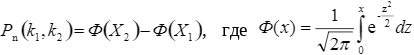- интегральная функция Муавра-Лапласа;