Для каждого варианта необходимо выделить множество Парето и сравнить содержащиеся в нем альтернативы с помощью метода опорных множеств, руководствуясь порядковой информацией Ω.

24 июля 2024
Управление проектами

Условие:

Имеется множество альтернатив X = { x1 , x2 ,..., xm }, оцениваемых по набору критериев F = { f1, f2 ,..., fn } с помощью единой шкалы (более предпочтительной считается более высокая оценка). Для каждого варианта необходимо выделить множество Парето и сравнить содержащиеся в нем альтернативы с помощью метода опорных множеств, руководствуясь порядковой информацией Ω.
Исходные данные:

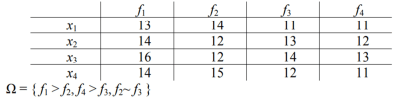
Необходимо выделить множество Парето и сравнить содержащиеся в нем альтернативы с помощью метода опорных множеств, руководствуясь порядковой информацией Ω = { f1 > f2, f4 > f3, f2~ f3 }.

Решение:

Сравнивая векторные оценки альтернатив по Парето, устанавливаем: x3 x2; x4 x1. Его элементы подлежат сравнению на основе заданной -информации. Введем следующие обозначения для векторных оценок альтернатив:

Y=F(x3)= (16,12,14,13)

Z=F(x4)= (14,15,12,11)

В качестве исходной оценки возьмем z и построим опорные множества для оценки Y.