Условие:
Доказать, что фактор группа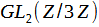 
по ее центру изоморфна группе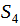 
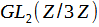– группа обратимых матриц (матрицы, определитель которых не равен 0) порядка 2 с элементами из множества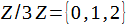 
Решение:
С другой стороны матрицу порядка 2 с элементами из множества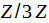 
можно рассматривать как линейный оператор, действующий на арифметическом векторном пространстве (то есть пространство 2-мерных столбцов с элементами из )