Группе из трех равноправных компаньонов необходимо принять оптимальное групповое решение, выбрав его из четырех возможных вариантов a один, a два, а три, а четыре. Каждое лицо группы по-разному оценивает возможные решения.

22 января 2025
Высшая математика

Условие:

Группе из трех равноправных компаньонов необходимо принять оптимальное групповое решение, выбрав его из четырех возможных вариантов a₁, a₂, а₃, а₄. Каждое лицо группы по-разному оценивает возможные решения. Эта оценка приведена ниже в таблице рангов, чем ниже ранг, тем предпочтение больше.

Ранжировка альтернатив.

Задачу необходимо решить методами Лапласа, Вальда, Сэведжа, Гурвица.

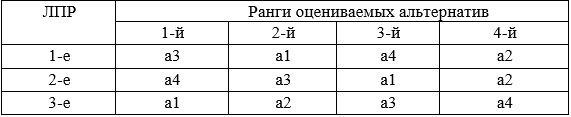
Решение:

Составим таблиц для применения критериев Лапласа, Вальда, Сэведжа, Гурвица:

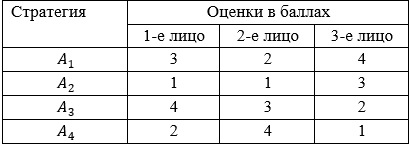
Метод Лапласа.

Согласно данному критерию все состояния природы равновероятны. В данном контексте это можно интерпретировать как равновероятные важности оценок всех трёх компаньонов. Соответственно, эти вероятности полагаем равными 1/3.