Используя экспериментальные данные, рассчитать коэффициенты корреляции между каждой парой параметров по формулам и внести данные в таблицу.
- Высшая математика
Условие:
Используя экспериментальные данные, рассчитать коэффициенты корреляции между каждой парой параметров по формулам и внести данные в таблицу. Далее устанавливаем статистические значимые линейные связи и строим граф корреляционных связей, и по нему выбираем параметр оптимизации и зависимые параметры, потом между этими параметрами рассчитываем коэффициент линейной связи, после чего составить вывод и дать анализ.
Исходные данные приведены в таблице 1.
Таблица 1 - Исходные данные
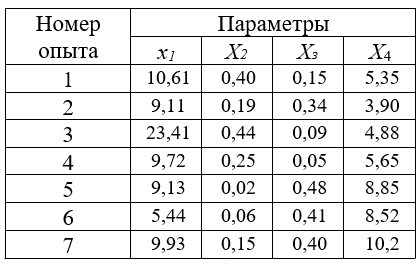
Корреляционный анализ позволяет установить статистические связи (как правило, линейные) между параметрами модели и оказывает значительную помощь при оптимизации в ситуациях со многими параметрами. Суть корреляционного анализа заключается в определении коэффициентов парной корреляции между каждыми двумя параметрами (попарно) на основании имеющихся экспериментальных данных. При наличии высокой корреляции между параметрами любой из них можно исключить из рассмотрения, так как он не содержит какой-либо дополнительной информации об объекте исследования, кроме полученной с помощью другого параметра. Исключать нужно те параметры, которые труднее определять экспериментально или физический смысл которых менее ясен.
Количественно статистические связи между параметрами оценивают с помощью коэффициента парной корреляции r, который является мерой тесноты линейной связи между двумя случайными величина ми. В общем случае его величина может меняться от минус 1 до 1. Если r равен 0, то связь либо вообще отсутствует, либо отлична от линейной. Если он равен минус 1 или 1, то связь идеально линейная. Знак коэффициента корреляции указывает на направление связи: увеличение одной из переменных при положительной корреляции влечет за собой увеличение, а при отрицательной - уменьшение другой.
Решение:
Коэффициент корреляции между парой параметров хк и хт определим по формуле [1]:
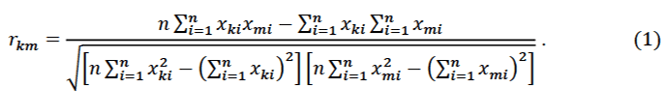
где n - число опытов. Составим расчетную таблицу:

Расчет значений коэффициентов корреляции:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства