1. Главная
  2. Библиотека
  3. Высшая математика
  4. Известны результаты независимых наблюдений над случайной величиной X. Необходимо: 1) Сгруппировать эти данные в интерва...

Известны результаты независимых наблюдений над случайной величиной X. Необходимо: 1) Сгруппировать эти данные в интервальную таблицу

«Известны результаты независимых наблюдений над случайной величиной X. Необходимо: 1) Сгруппировать эти данные в интервальную таблицу»
  • Высшая математика

Условие:

Известны результаты независимых наблюдений над случайной величиной X. Необходимо:

1) Сгруппировать эти данные в интервальную таблицу

2) Построить гистограмму, полигон частот и эмпирическую функцию распределения

3) Найти несмещенную оценку математического ожидания и дисперсии случайной величины X

4) Найти интервальные оценки математического ожидания и дисперсии случайной величины X с надежностью γ=0,9 и γ=0,95

5) Выдвинуть гипотезу о законе распределения случайной величины X  и проверить ее по критерию χ2  (Пирсона) при уровне значимости α=0,05.

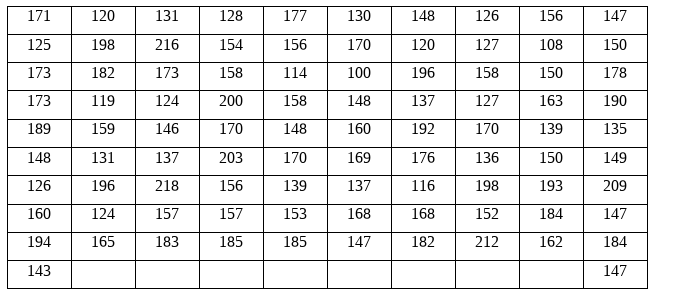
Решение:

1) Сгруппируем данные в интервальную таблицу. Для этого найдем:

а) Объем выборки n=92; xmin =100; xmax =218

б) Количество интервалов по формуле Стерджеса:

k=1+3,322∙ lg 92 =1+6,524=7,5248

в) Длина интервала:

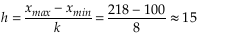
г) xнач = xmin -0,5∙h=100-7,5=92,5

Построим интервальный ряд:

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я