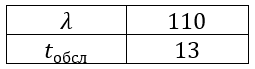
На сортировочной станции работают две сортировочные горки. На расформирование прибывает простейший поток составов с интенсивностью λ составов в сутки. Горочный технологический интервал составляет

26 марта 2025
Высшая математика

Условие:

На сортировочной станции работают две сортировочные горки. На расформирование прибывает простейший поток составов с интенсивностью λ составов в сутки. Горочный технологический интервал составляет t_мин (t_обсл ). Время обработки распределено по показательному закону. Очередь не ограничена.

1. Описать состояния системы, построить граф состояний.

2. Найти вероятности состояний для стационарного случая и показатели эффективности работы сортировочной станции. Определить процент составов, идущих сразу на обработку.

3. Найти величину среднесуточного штрафа за пребывание составов в очереди на внешних путях, если известно, что в парке сортировочной станции могут находиться одновременно не более трех составов. За один час пребывания на внешних путях станция платит штраф 100 у.е.

Решение:

1. Запишем состояния СМО:

S₀ СМО свободна, составов на сортировочной горке нет;
S₁ одна из сортировочных горок занята, очереди нет;
S₂ заняты две сортировочные горки, очереди нет;
S₃ заняты все две сортировочные горки, причем один состав в очереди;

S_(n+r) две горки (n=2) заняты обслуживанием состава, r составов в очереди и так далее.

Теоретически число состояний не ограничено (бесконечно).

Граф состояний примет вид: