Условие:
Построить на плоскости область решений системы линейных неравенств и геометрически найти наименьшее и наибольшее значение линейной функции.
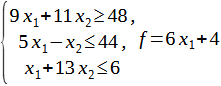
Решение:
Для этого в неравенствах системы ограничений перейдем к равенствам и построим соответствующие прямые:
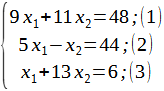
Прямые линии строим по двум точкам. Тогда допустимую область задачи можно изобразить графически как множество точек плоскости, координаты которых удовлетворяют сразу всем неравенствам задачи.
Чтобы определить расположение соответствующей полуплоскости относительно граничной прямой, подставим координ...