Приведена выборка 108 результатов измерений случайной величины икс. Построить интервальный вариационный ряд по частотам, относительным частотам и накопленным частотам.
- Высшая математика
Условие:
Приведена выборка 108 результатов измерений случайной величины Х
Построить интервальный вариационный ряд (ряд 1) по частотам, относительным частотам и накопленным частотам.
От ряда 1 перейти к точечному вариационному ряду (ряд 2).
Начертить полигоны частот и относительных частот, кумуляту (по ряду 2) и гистограммы частот и относительных частот (по ряду 1).
Записать аналитически и построить графически статистическую функцию распределения (по ряду 2).
Найти выборочные средние: среднюю арифметическую, среднюю геометрическую, среднюю гармоническую; выборочную дисперсию, выборочное среднеквадратическое отклонение, коэффициенты вариации и асимметрии (по ряду 2).
Определить моду и медиану графически и аналитически (по рядам 1 и 2).
На основе анализа гистограммы и статистической функции распределения оценить близость эмпирического распределения к нормальному закону, проверить гипотезу о том, что случайная величина Х имеет нормальный закон распределения по критерию Пирсона (χ2).
При заданной надежности γ = 0,95 построить доверительные интервалы для неизвестного математического ожидания а, неизвестной дисперсии D и среднего квадратического отклонения σ случайной величины Х в предположении, что выборка извлечена из генеральной совокупности, подчиненной нормальному закону.

Решение:
Число интервалов разбиения выборки определяется поформуле Стерджеса.
n = 1 + 3,322 lg N = 7.
Минимальное значение выборки:
xmin = 410.
Максимальное значение выборки:
xmax = 846.
Размах выборки:
R = xmax xmin = 436.
Размер интервала разбиения:
= R/n = 62.
Распределив значения выборки по интервалам, запишем интервальный вариационный ряд 1 в таблицу.
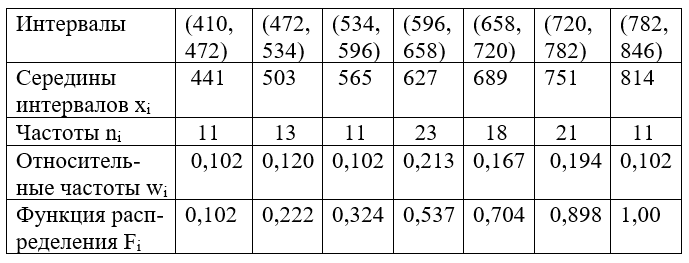
В таблице указаны также частоты, относительные ч...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства