Привести общее уравнение кривой второго порядка игрек в квадрате минус 2 игрек плюс 3 икс минус 3 равно 0 к каноническому виду и найти точки пересечения её с прямой икс плюс игрек плюс 1 равно 0. Построить графики кривой и прямой.

Чтобы привести уравнение кривой к каноническому виду, выделим полный квадрат в многочлене второго порядка:

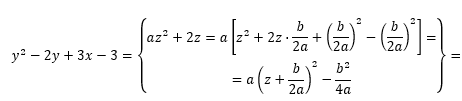(y² - 2y) + 3x - 3 = ( y² - 2 * y * 1 + 1² - 1²) + 3x - 3 = (y² - 2 * y * 1 + 1²) - 1 + 3x - 3 = (y - 1)² + 3x - 4.

Пользуясь полученным результатом, данное уравнение кривой можно преобразовать к каноническому виду (7) уравнения парабол...