Проинтегрировать систему. Продифференцируем первое уравнение по x. В результате, получили линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами.
«Проинтегрировать систему. Продифференцируем первое уравнение по x. В результате, получили линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами.»
- Высшая математика
Условие:
Проинтегрировать систему
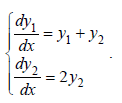
Решение:
Продифференцируем первое уравнение по x :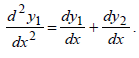
В полученное уравнение подставим из первого уравнения и из второго уравнения, тогдаВ результате, получили систему:Из первого уравнения выразим: (*)и подставим во второе уравнение:В результате, получили линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его характеристическое уравнение имеет вид: ; находим кор...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э