Условие:
Случайная величина задана интегральной функцией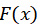 
. Требуется:
1) определить значение параметра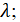 
2) найти дифференциальную функцию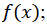 
3) вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X;
4) построить графики интегральной и дифференциальной функций;
5) найти вероятность того, что случайная величина попадает в интервал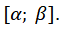 
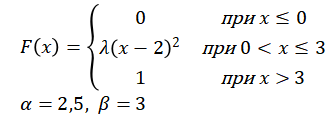
Решение:
1) Так как по условию случайная величина непрерывна, то по определению её функция распределения непрерывна на всей числовой оси. Из условия следует, что функция распределения может иметь разрывы только в двух точках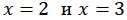 
. Для непрерывности достаточно, чтобы предел слева в этих точках равнялся пределу справа. Найдём эти пределы: