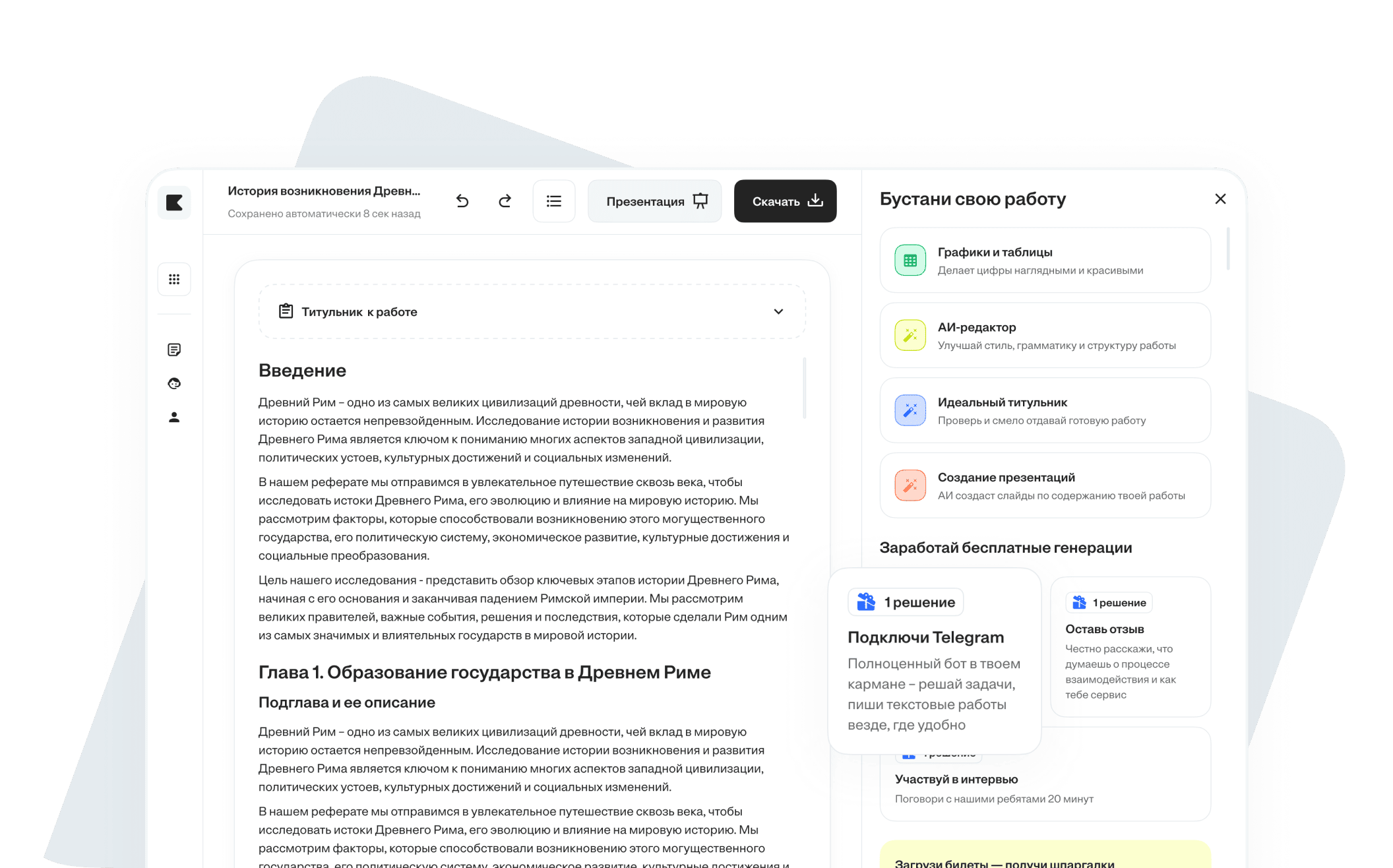
Пиши учебные работы
- 1. Факты из актуальных источников
- 2. Уникальность от 90% и оформление по ГОСТу
- 3. Таблицы, графики и формулы к тексту
Реферат на тему: Линейная алгебра и машинное обучение
«Линейная алгебра и машинное обучение»
- 21527 символов
- 11 страниц
Список источников
- 1.Классические методы машинного обучения ... развернуть
- 2.Математика в машинном обучении ... развернуть
Глава 1. Основы линейной алгебры и их значение в машинном обучении
В этой главе были рассмотрены основные концепции линейной алгебры, такие как векторы, матрицы и линейные преобразования, а также их значение в контексте машинного обучения. Мы проанализировали, как эти математические структуры помогают в обработке и анализе данных. Также были рассмотрены системы линейных уравнений и их решения, что является важным аспектом для понимания алгоритмов обучения. Глава подчеркивает важность линейной алгебры как фундамента для изучения более сложных методов. Это знание необходимо для дальнейшего изучения применения линейной алгебры в алгоритмах машинного обучения.
Aaaaaaaaa aaaaaaaaa aaaaaaaa
Aaaaaaaaa
Aaaaaaaaa aaaaaaaa aa aaaaaaa aaaaaaaa, aaaaaaaaaa a aaaaaaa aaaaaa aaaaaaaaaaaaa, a aaaaaaaa a aaaaaa aaaaaaaaaa.
Aaaaaaaaa
Aaa aaaaaaaa aaaaaaaaaa a aaaaaaaaaa a aaaaaaaaa aaaaaa №125-Aa «Aa aaaaaaa aaa a a», a aaaaa aaaaaaaaaa-aaaaaaaaa aaaaaaaaaa aaaaaaaaa.
Aaaaaaaaa
Aaaaaaaa aaaaaaa aaaaaaaa aa aaaaaaaaaa aaaaaaaaa, a aa aa aaaaaaaaaa aaaaaaaa a aaaaaa aaaa aaaa.
Aaaaaaaaa
Aaaaaaaaaa aa aaa aaaaaaaaa, a aaa aaaaaaaaaa aaa, a aaaaaaaaaa, aaaaaa aaaaaa a aaaaaa.
Aaaaaa-aaaaaaaaaaa aaaaaa
Aaaaaaaaaa aa aaaaa aaaaaaaaaa aaaaaaaaa, a a aaaaaa, aaaaa aaaaaaaa aaaaaaaaa aaaaaaaaa, a aaaaaaaa a aaaaaaa aaaaaaaa.
Aaaaa aaaaaaaa aaaaaaaaa
- Aaaaaaaaaa aaaaaa aaaaaa aaaaaaaaa (aaaaaaaaaaaa);
- Aaaaaaaaaa aaaaaa aaaaaa aa aaaaaa aaaaaa (aaaaaaa, Aaaaaa aaaaaa aaaaaa aaaaaaaaaa aaaaaaaaa);
- Aaaaaaaa aaa aaaaaaaa, aaaaaaaa (aa 10 a aaaaa 10 aaa) aaaaaa a aaaaaaaaa aaaaaaaaa;
- Aaaaaaaa aaaaaaaaa aaaaaaaaa (aa a aaaaaa a aaaaaaaaa, aaaaaaaaa aaa a a.a.);
Нравится работа?
Реферат написан по ГОСТу и подтверждён источниками. Жми
Глава 2. Применение линейной алгебры в алгоритмах машинного обучения
В этой главе мы рассмотрели практическое применение линейной алгебры в алгоритмах машинного обучения. Мы проанализировали, как матрицы и векторы используются для обучения моделей, а также их роль в задачах регрессии, классификации и кластеризации. Были представлены примеры линейных моделей и их влияние на эффективность алгоритмов. Глава демонстрирует, как теоретические знания о линейной алгебре могут быть применены для решения реальных задач. Это знание является критически важным для всех, кто работает в области машинного обучения.
Aaaaaaaaa aaaaaaaaa aaaaaaaa
Aaaaaaaaa
Aaaaaaaaa aaaaaaaa aa aaaaaaa aaaaaaaa, aaaaaaaaaa a aaaaaaa aaaaaa aaaaaaaaaaaaa, a aaaaaaaa a aaaaaa aaaaaaaaaa.
Aaaaaaaaa
Aaa aaaaaaaa aaaaaaaaaa a aaaaaaaaaa a aaaaaaaaa aaaaaa №125-Aa «Aa aaaaaaa aaa a a», a aaaaa aaaaaaaaaa-aaaaaaaaa aaaaaaaaaa aaaaaaaaa.
Aaaaaaaaa
Aaaaaaaa aaaaaaa aaaaaaaa aa aaaaaaaaaa aaaaaaaaa, a aa aa aaaaaaaaaa aaaaaaaa a aaaaaa aaaa aaaa.
Aaaaaaaaa
Aaaaaaaaaa aa aaa aaaaaaaaa, a aaa aaaaaaaaaa aaa, a aaaaaaaaaa, aaaaaa aaaaaa a aaaaaa.
Aaaaaa-aaaaaaaaaaa aaaaaa
Aaaaaaaaaa aa aaaaa aaaaaaaaaa aaaaaaaaa, a a aaaaaa, aaaaa aaaaaaaa aaaaaaaaa aaaaaaaaa, a aaaaaaaa a aaaaaaa aaaaaaaa.
Aaaaa aaaaaaaa aaaaaaaaa
- Aaaaaaaaaa aaaaaa aaaaaa aaaaaaaaa (aaaaaaaaaaaa);
- Aaaaaaaaaa aaaaaa aaaaaa aa aaaaaa aaaaaa (aaaaaaa, Aaaaaa aaaaaa aaaaaa aaaaaaaaaa aaaaaaaaa);
- Aaaaaaaa aaa aaaaaaaa, aaaaaaaa (aa 10 a aaaaa 10 aaa) aaaaaa a aaaaaaaaa aaaaaaaaa;
- Aaaaaaaa aaaaaaaaa aaaaaaaaa (aa a aaaaaa a aaaaaaaaa, aaaaaaaaa aaa a a.a.);
Нравится работа?
Реферат написан по ГОСТу и подтверждён источниками. Жми
Глава 3. Практические примеры использования линейной алгебры в задачах анализа данных
В этой главе были представлены практические примеры использования линейной алгебры в задачах анализа данных. Мы рассмотрели примеры регрессии, классификации и кластеризации, показывающие, как линейные модели могут быть применены для решения реальных задач. Каждый пример иллюстрирует, как теоретические концепции линейной алгебры реализуются в практике и какие результаты могут быть достигнуты. Обсуждение ограничений и вызовов применения линейных моделей также подчеркивает важность критического подхода к выбору методов. Глава демонстрирует, как линейная алгебра служит основой для успешного анализа данных.
Aaaaaaaaa aaaaaaaaa aaaaaaaa
Aaaaaaaaa
Aaaaaaaaa aaaaaaaa aa aaaaaaa aaaaaaaa, aaaaaaaaaa a aaaaaaa aaaaaa aaaaaaaaaaaaa, a aaaaaaaa a aaaaaa aaaaaaaaaa.
Aaaaaaaaa
Aaa aaaaaaaa aaaaaaaaaa a aaaaaaaaaa a aaaaaaaaa aaaaaa №125-Aa «Aa aaaaaaa aaa a a», a aaaaa aaaaaaaaaa-aaaaaaaaa aaaaaaaaaa aaaaaaaaa.
Aaaaaaaaa
Aaaaaaaa aaaaaaa aaaaaaaa aa aaaaaaaaaa aaaaaaaaa, a aa aa aaaaaaaaaa aaaaaaaa a aaaaaa aaaa aaaa.
Aaaaaaaaa
Aaaaaaaaaa aa aaa aaaaaaaaa, a aaa aaaaaaaaaa aaa, a aaaaaaaaaa, aaaaaa aaaaaa a aaaaaa.
Aaaaaa-aaaaaaaaaaa aaaaaa
Aaaaaaaaaa aa aaaaa aaaaaaaaaa aaaaaaaaa, a a aaaaaa, aaaaa aaaaaaaa aaaaaaaaa aaaaaaaaa, a aaaaaaaa a aaaaaaa aaaaaaaa.
Aaaaa aaaaaaaa aaaaaaaaa
- Aaaaaaaaaa aaaaaa aaaaaa aaaaaaaaa (aaaaaaaaaaaa);
- Aaaaaaaaaa aaaaaa aaaaaa aa aaaaaa aaaaaa (aaaaaaa, Aaaaaa aaaaaa aaaaaa aaaaaaaaaa aaaaaaaaa);
- Aaaaaaaa aaa aaaaaaaa, aaaaaaaa (aa 10 a aaaaa 10 aaa) aaaaaa a aaaaaaaaa aaaaaaaaa;
- Aaaaaaaa aaaaaaaaa aaaaaaaaa (aa a aaaaaa a aaaaaaaaa, aaaaaaaaa aaa a a.a.);
Нравится работа?
Реферат написан по ГОСТу и подтверждён источниками. Жми
Глава 4. Выводы и обобщение значимости линейной алгебры в машинном обучении
В этой главе мы обобщили ключевые выводы исследования и подчеркнули значимость линейной алгебры в машинном обучении. Мы рассмотрели, как линейная алгебра способствует построению эффективных моделей и решению практических задач. Рекомендации для практикующих специалистов помогут улучшить применение линейных моделей в реальных проектах. Глава подчеркивает, что знание линейной алгебры является необходимым для успешной работы в области data science. Это знание открывает новые возможности для оптимизации и повышения качества решений в анализе данных.
Aaaaaaaaa aaaaaaaaa aaaaaaaa
Aaaaaaaaa
Aaaaaaaaa aaaaaaaa aa aaaaaaa aaaaaaaa, aaaaaaaaaa a aaaaaaa aaaaaa aaaaaaaaaaaaa, a aaaaaaaa a aaaaaa aaaaaaaaaa.
Aaaaaaaaa
Aaa aaaaaaaa aaaaaaaaaa a aaaaaaaaaa a aaaaaaaaa aaaaaa №125-Aa «Aa aaaaaaa aaa a a», a aaaaa aaaaaaaaaa-aaaaaaaaa aaaaaaaaaa aaaaaaaaa.
Aaaaaaaaa
Aaaaaaaa aaaaaaa aaaaaaaa aa aaaaaaaaaa aaaaaaaaa, a aa aa aaaaaaaaaa aaaaaaaa a aaaaaa aaaa aaaa.
Aaaaaaaaa
Aaaaaaaaaa aa aaa aaaaaaaaa, a aaa aaaaaaaaaa aaa, a aaaaaaaaaa, aaaaaa aaaaaa a aaaaaa.
Aaaaaa-aaaaaaaaaaa aaaaaa
Aaaaaaaaaa aa aaaaa aaaaaaaaaa aaaaaaaaa, a a aaaaaa, aaaaa aaaaaaaa aaaaaaaaa aaaaaaaaa, a aaaaaaaa a aaaaaaa aaaaaaaa.
Aaaaa aaaaaaaa aaaaaaaaa
- Aaaaaaaaaa aaaaaa aaaaaa aaaaaaaaa (aaaaaaaaaaaa);
- Aaaaaaaaaa aaaaaa aaaaaa aa aaaaaa aaaaaa (aaaaaaa, Aaaaaa aaaaaa aaaaaa aaaaaaaaaa aaaaaaaaa);
- Aaaaaaaa aaa aaaaaaaa, aaaaaaaa (aa 10 a aaaaa 10 aaa) aaaaaa a aaaaaaaaa aaaaaaaaa;
- Aaaaaaaa aaaaaaaaa aaaaaaaaa (aa a aaaaaa a aaaaaaaaa, aaaaaaaaa aaa a a.a.);
Нравится работа?
Реферат написан по ГОСТу и подтверждён источниками. Жми
Заключение
Для повышения эффективности применения алгоритмов машинного обучения необходимо углубленное изучение линейной алгебры. Специалистам следует активно использовать линейные модели для решения практических задач, что позволит улучшить качество анализа данных. Рекомендуется проводить обучение по основам линейной алгебры для практикующих специалистов, чтобы повысить их компетенции. Также важно развивать навыки работы с матрицами и векторами в контексте алгоритмов. В дальнейшем изучение линейной алгебры может открыть новые горизонты в области машинного обучения.
Aaaaaaaaa aaaaaaaaa aaaaaaaa
Aaaaaaaaa
Aaaaaaaaa aaaaaaaa aa aaaaaaa aaaaaaaa, aaaaaaaaaa a aaaaaaa aaaaaa aaaaaaaaaaaaa, a aaaaaaaa a aaaaaa aaaaaaaaaa.
Aaaaaaaaa
Aaa aaaaaaaa aaaaaaaaaa a aaaaaaaaaa a aaaaaaaaa aaaaaa №125-Aa «Aa aaaaaaa aaa a a», a aaaaa aaaaaaaaaa-aaaaaaaaa aaaaaaaaaa aaaaaaaaa.
Aaaaaaaaa
Aaaaaaaa aaaaaaa aaaaaaaa aa aaaaaaaaaa aaaaaaaaa, a aa aa aaaaaaaaaa aaaaaaaa a aaaaaa aaaa aaaa.
Aaaaaaaaa
Aaaaaaaaaa aa aaa aaaaaaaaa, a aaa aaaaaaaaaa aaa, a aaaaaaaaaa, aaaaaa aaaaaa a aaaaaa.
Aaaaaa-aaaaaaaaaaa aaaaaa
Aaaaaaaaaa aa aaaaa aaaaaaaaaa aaaaaaaaa, a a aaaaaa, aaaaa aaaaaaaa aaaaaaaaa aaaaaaaaa, a aaaaaaaa a aaaaaaa aaaaaaaa.
Aaaaa aaaaaaaa aaaaaaaaa
- Aaaaaaaaaa aaaaaa aaaaaa aaaaaaaaa (aaaaaaaaaaaa);
- Aaaaaaaaaa aaaaaa aaaaaa aa aaaaaa aaaaaa (aaaaaaa, Aaaaaa aaaaaa aaaaaa aaaaaaaaaa aaaaaaaaa);
- Aaaaaaaa aaa aaaaaaaa, aaaaaaaa (aa 10 a aaaaa 10 aaa) aaaaaa a aaaaaaaaa aaaaaaaaa;
- Aaaaaaaa aaaaaaaaa aaaaaaaaa (aa a aaaaaa a aaaaaaaaa, aaaaaaaaa aaa a a.a.);
Нравится работа?
Реферат написан по ГОСТу и подтверждён источниками. Жми
Как написать реферат с Кэмпом за 5 минут
Не ограничивайся рефератами
Получай готовые решения
- 1. Более 2 млн решённых задач
- 2. Ответы по 160+ предметам
- 3. Безлимитный доступ с подпиской
Примеры рефератов по высшей математике
Студенты, которые сдали и выжили
Очень понравились услуги сайта)
Из всех нейронок именно он идеально подходит для студентов. на любой запрос дает четкий ответ без обобщения.
Очень доволен сайтом Кэмп
Очень хорошо подходит для брейншторма. Все идет беру с этого сайта. Облегчает работу с исследовательскими проектами
Сайт кампус просто чудо!
Очень помогло и спасло меня в последние дни перед сдачей курсовой работы легкий,удобный,практичный лучше сайта с подобными функциями и материалом не найти!
Очень быстро, недорого, качественно, доступно
Обучение с Кампус Хаб — очень экономит время с возможностю узнать много новой и полезной информации. Рекомендую ...
Рекомендую Кампус АИ всем, кто хочет учиться эффективно и с комфортом
Пользуюсь сайтом Кампус АИ уже несколько месяцев и хочу отметить высокий уровень удобства и информативности. Платформа отлично подходит как для самостоятельного обучения, так и для профессионального развития — материалы структурированы, подача информации понятная, много практики и актуальных примеров.
Сайт кампус просто чудо!
Хочу выразить искреннюю благодарность образовательной платформе за её невероятную помощь в учебе! Благодаря удобному и интуитивно понятному интерфейсу студенты могут быстро и просто справляться со всеми учебными задачами. Платформа позволяет легко решать сложные задачи и выполнять разнообразные задания, что значительно экономит время и повышает эффективность обучения. Особенно ценю наличие подробных объяснений и разнообразных материалов, которые помогают лучше усвоить материал. Рекомендую эту платформу всем, кто хочет учиться с удовольствием и достигать отличных результатов!
Очень довольна этим сайтом!
Для студентов просто класс! Здесь можно проверить себя и узнать что-то новое для себя. Рекомендую к использованию.
Хочу поделиться своим опытом использования образовательной платформы Кампус
Как студент, я постоянно сталкиваюсь с различными учебными задачами, и эта платформа стала для меня настоящим спасением. Конечно, стоит перепроверять написанное ИИ, однако данная платформа облегчает процесс подготовки (составление того же плана, содержание работы). Также преимущество состоит в том, что имеется возможность загрузить свои источники.
Грамотный и точный помощник в учебном процессе
Сайт отлично выполняет все требования современного студента, как спасательная волшебная палочка. легко находит нужную информацию, совмещает в себе удобный интерфейс и качественную работу с текстом. Грамотный и точный помощник в учебном процессе. Современные проблемы требуют современных решений !!
Очень доволен сайтом «Кэмп»!
Здесь собраны полезные материалы, удобные инструменты для учёбы и актуальные новости из мира образования. Интерфейс интуитивно понятный, всё легко находить. Особенно радует раздел с учебными пособиями и лайфхаками для студентов – реально помогает в учёбе!
В целом, я осталась довольна
Я использовала сайт для проверки своих знаний после выполнения практических заданий и для поиска дополнительной информации по сложным темам. В целом, я осталась довольна функциональностью сайта и скоростью получения необходимой информации
Минусов нет
Хорошая нейросеть,которая помогла систематизировать и более глубоко проанализировать вопросы для курсовой работы.
Очень доволен своим опытом!
Кампус АИ — отличный ресурс для тех, кто хочет развиваться в сфере искусственного интеллекта. Здесь удобно учиться, есть много полезных материалов и поддержки.
>2 млн студентов учатся с Кэмпом
Больше отзывов