1. Главная
  2. Библиотека
  3. Автоматизация технологических процессов
  4. Дано уравнение эф от икс равно ноль. Отделить корни в интервале [а, бэ] и уточнить один из них. Разработать блок-схему алг...

Дано уравнение эф от икс равно ноль. Отделить корни в интервале [а, бэ] и уточнить один из них. Разработать блок-схему алго­ритма используемого метода. Результаты представить в виде таблиц и гра­фиков.

«Дано уравнение эф от икс равно ноль. Отделить корни в интервале [а, бэ] и уточнить один из них. Разработать блок-схему алго­ритма используемого метода. Результаты представить в виде таблиц и гра­фиков.»
  • Автоматизация технологических процессов

Условие:

Дано уравнение f(х) = 0, Отделить корни в интервале [а, b] и уточнить один из них (любой на выбор) заданным методом. Разработать блок-схему алго­ритма используемого метода. Результаты представить в виде таблиц (i - хi - f(хi)) и гра­фиков в координатах хi - f(хi), где i – номер шага (итерации).

Отделение корней произвести только графическим методом.

Уточнение корней произвести одним методом. Метод уточнения корней выбрать по числу N6+1 из общего списка методов:

N6 = 47/6 = 7(остаток 5); N6 + 1 = 5+1 = 6

Используем метод деления отрезка пополам.

Заданная функция f(x)=-1*1.5x + sin(4x+2); интервал [-10;5]

Дополнительные данные: погрешность решения принять равной ε = 0.01.

Решение:

3.1. Отделение корней функции на интервале [-10;5] графическим методом

Построим график функции:

f(x)=-1*1.5x + sin(4x+2) на интервале [-10;5]

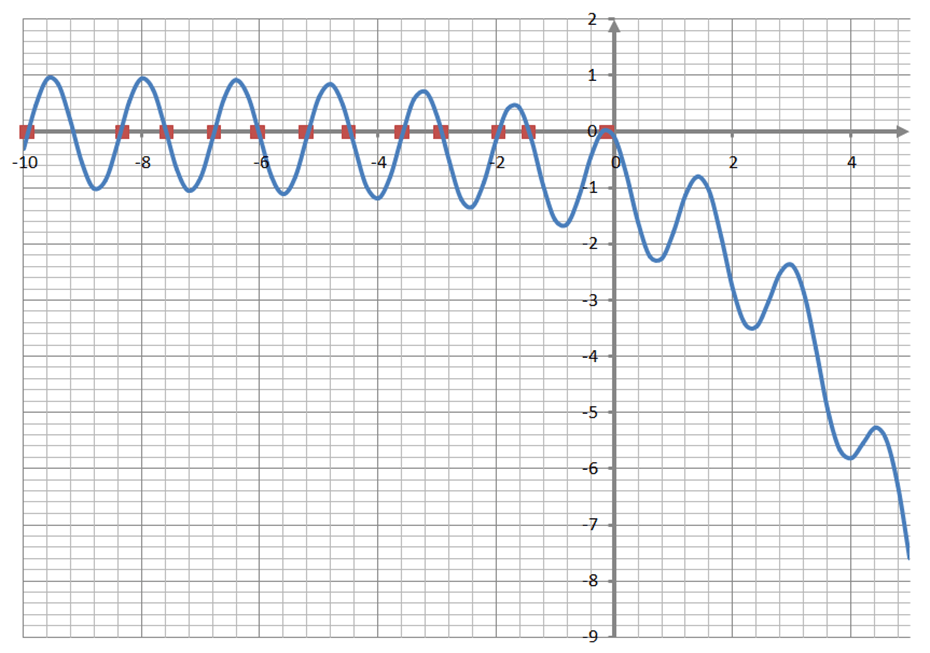
Рис.3 - Определение корней функции графическим методом

У функции -1*1.5x + sin(4x+2) на интервале [-10;5] имеется 12 корней:

x1=-9.93; x2=-8.33; x3=-7.58; x4=6.78; x5=-6.02; x6=-5.2; x7=-4.5; x8=-3.58; x9=-2.92; x10=-1.97; x11=-1.46; x12=-0.12.

3.2....

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я