1. Главная
  2. Библиотека
  3. Детали машин
  4. Изделие состоит из N групп узлов. Отказы узлов первой группы подчинены экспоненциальному закону с интенсивностью отказов λ...

Изделие состоит из N групп узлов. Отказы узлов первой группы подчинены экспоненциальному закону с интенсивностью отказов λ

«Изделие состоит из N групп узлов. Отказы узлов первой группы подчинены экспоненциальному закону с интенсивностью отказов λ»
  • Детали машин

Условие:

Изделие состоит из N групп узлов. Отказы узлов первой группы подчинены экспоненциальному закону с интенсивностью отказов λ , отказы узлов второй группы – нормальному закону с параметрами T1 и σ и отказы узлов третьей группы – закону Вейбулла с параметрами λ0 и k . Вычислить количественные характеристики надежности (плотность распределения отказов, интенсивность отказов и среднюю наработку до первого отказа) для каждой из групп узлов.

Исходные данные:

Требуется определить вероятность безотказной работы изделия в течении времени t .

Решение:

А. Экспоненциальный закон распределения (параметры , t)

Частота отказов (плотность распределения), по формуле:

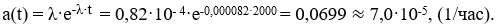
Вероятность безотказной работы по формуле:

Интенсивность отказов: = 0,8210-4 = const, 1/час...

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я