Условие задачи
Механическая мастерская завода с тремя постами (каналами) выполняет ремонт малой механизации.
Поток неисправных механизмов, прибывающих в мастерскую, - пуассоновский и имеет интенсивность λ = 2,5 механизма в сутки, среднее время ремонта одного механизма распределено по показательном у закону и равно t-= 0,5 сут. Предположим, что другой мастерской на заводе нет, и, значит, очередь механизмов перед мастерской может расти практически неограниченно.
Требуется вычислить следующие предельные значения вероятностных характеристик системы:
- вероятности состояний системы;
- среднее число заявок в очереди на обслуживание;
- среднее число находящихся в системе заявок;
- среднюю продолжительность пребывания заявки в очереди;
- среднюю продолжительность пребывания заявки в системе.
Ответ
1. Определим параметр потока обслуживаний
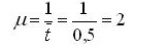
2. Приведенная интенсивность потока заявок
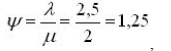
при этом
