1. Главная
  2. Библиотека
  3. Другое
  4. Предприятие располагает двумя видами сырья S1 и S2 соответственно в количествах b1, b2 условных единиц. Из этого сырья мож...

Предприятие располагает двумя видами сырья S1 и S2 соответственно в количествах b1, b2 условных единиц. Из этого сырья может быть изготовлено два вида продукции Р1, Р2. Для изготовления единицы Pj-го вида продукции необходимо aij единиц Si-го (i=1,2)

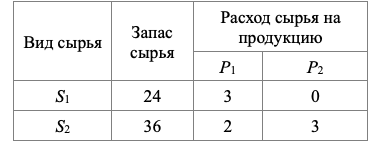
«Предприятие располагает двумя видами сырья S1 и S2 соответственно в количествах b1, b2 условных единиц. Из этого сырья может быть изготовлено два вида продукции Р1, Р2. Для изготовления единицы Pj-го вида продукции необходимо aij единиц Si-го (i=1,2)»
  • Другое

Условие:

Предприятие располагает двумя видами сырья S1 и S2 соответственно в количествах b1, b2 условных единиц. Из этого сырья может быть изготовлено два вида продукции Р1, Р2. Для изготовления единицы Pj-го вида продукции необходимо aij единиц Si-го (i=1,2) вида сырья. От реализации одной единицы каждого вида продукции предприятие получает доход 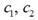  ден. ед.  

1. Найти оптимальный план геометрическим методом.  

2. Найти оптимальный план симплексным методом.   

3. Сформулировать экономически, записать и решить двойственную задачу. Пояснить экономический смысл полученных объективно обусловленных оценок.  

С=(5,4) 

Решение:

Пусть продукции Р1 необходимо выпускать х1, продукции Р2 х2, тогда ограничения по

сырью S1: 3x124,

сырью S2: 2x1+3x236,

по неотрицательности переменных:

x1 0,

x2 0.

Доход определяется как F=5x1+4x2, который необходимо максимизировать.

Математическая модель имеет вид:

F = 5x1+4x2 max

3x124,
2x1+3x236,

x1 0,

x2 0.

Решим задачу графически.

Необходимо найти максимальное значение целевой функции
F = 5x1+4x2 max при системе ограничений:

3x124, (1)

2x1+3x236, (2)

x1 0, (3)

x2 0, (4)

Шаг №1. Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и опред...

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я